
命题![]() :“函数
:“函数![]() 在区间
在区间![]() 上递增”;命题
上递增”;命题![]() :“
:“ ![]() 在区间
在区间![]() 上递增”。若命题
上递增”。若命题![]() 与命题
与命题![]() 有且仅有一个真,求实数
有且仅有一个真,求实数![]() 的集合。
的集合。
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源:2014届安徽省高三上学期第一次月考文科数学试卷(解析版) 题型:填空题
给出下列五个命题:
①函数 在区间
在区间 上存在零点;
上存在零点;
②若 ,则函数
,则函数 在
在 处取得极值;
处取得极值;
③“ ”是“函数
”是“函数 在定义域上是奇函数”的充分不必要条件;
在定义域上是奇函数”的充分不必要条件;
④函数 的图像与函数
的图像与函数 的图像关于
的图像关于 轴对称;
轴对称;
⑤满足条件AC= ,AB =1的三角形△ABC有两个.其中正确命题的是 .
,AB =1的三角形△ABC有两个.其中正确命题的是 .
查看答案和解析>>
科目:高中数学 来源:2013届福建省高二下学期第二次月考文科数学试卷(解析版) 题型:解答题
设命题 :函数
:函数 在区间
在区间 上单调递减;命题
上单调递减;命题 :函数
:函数 的定义域是
的定义域是 .如果命题
.如果命题 为真命题,
为真命题, 为假命题,求
为假命题,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河南省豫南九校高三第四次联考文科数学 题型:填空题
给出下列四个命题:
①函数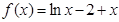 在区间
在区间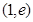 上存在零点;
上存在零点;
②若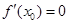 ,则函数
,则函数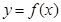 在
在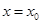 处取得极值;
处取得极值;
③若
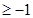 ,则函数
,则函数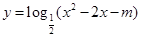 的值域为
的值域为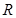 ;
;
④“ ”是“函数
”是“函数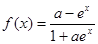 在定义域上是奇函数”的充分不必要条件。
在定义域上是奇函数”的充分不必要条件。
以上命题正确的是 (写出所有正确命题的编号).
查看答案和解析>>
科目:高中数学 来源:2011-2012学年安徽省高三第一次质量检测理科数学 题型:解答题
(本小题满分13分)已知命题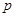 :函数
:函数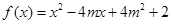 在区间
在区间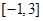 上的最小值等于2;命题
上的最小值等于2;命题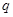 :不等式
:不等式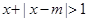 对于任意
对于任意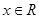 恒成立,如果上述两命题中有且仅有一个真命题,试求实数
恒成立,如果上述两命题中有且仅有一个真命题,试求实数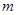 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年北京市高三上学期统考二理科数学试卷 题型:选择题
函数
 ,给出下列四个命题:
,给出下列四个命题:
①函数在区间 上是减函数;
上是减函数;
②直线 是函数图象的一条对称轴;
是函数图象的一条对称轴;
③函数 的图象可由函数
的图象可由函数 的图象向左平移
的图象向左平移 而得到;
而得到;
④若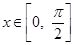 ,则
,则 的值域是[0,
的值域是[0, ]。
]。
其中正确命题的个数是
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com