练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    证明f(x)=在(0,+∞)上是减函数.

    思路分析:可采用定义法和求导法两种方法来解题,体会求导法在解决函数单调性问题上的优越性.

    证明:法一:任取两个数x1,x2∈(0,+∞),设x1＜x2,则

    f(x1)-f(x2)=-=,

    ∵x1＞0,x2＞0且x1＜x2,∴f(x1)-f(x2)＞0.∴f(x1)＞f(x2).

    ∴f(x)在(0,+∞)上是减函数.

    法二:f′(x)=,

    ∵x＞0,∴f′(x)＜0.

    ∴f(x)在(0,+∞)上是减函数.

        辨析比较 比较一下两种方法,用求导证明更简捷一些.如果是更复杂的函数,用导数的符号判断函数的单调性更能显示出它的优越性.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2013-2014学年湖北省武汉市高三11月调考理科数学试卷（解析版） 题型：解答题

    已知函数f(x)的导函数为f ′(x)，且对任意x＞0，都有f ′(x)＞．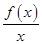

    （Ⅰ）判断函数F(x)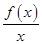＝在(0，＋∞)上的单调性；

    （Ⅱ）设x1，x2∈(0，＋∞)，证明：f(x1)＋f(x2)＜f(x1＋x2)；

    （Ⅲ）请将（Ⅱ）中的结论推广到一般形式，并证明你所推广的结论．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届山东省济宁市高一10月月考数学试卷（解析版） 题型：解答题

    判断并利用定义证明f(x)＝在(－∞，0)上的增减性．

     

    查看答案和解析>>

    科目：高中数学 来源：2012届江西省南昌市高三第一次模拟测试卷理科数学试卷 题型：填空题

    已知向量p＝(－cos 2x，a)，q＝(a,2－sin 2x)，函数f(x)＝p·q－5(a∈R，a≠0)

    (1)求函数f(x)(x∈R)的值域；

    (2)当a＝2时，若对任意的t∈R，函数y＝f(x)，x∈(t，t＋b]的图像与直线y＝－1有且仅有两个不同的交点，试确定b的值(不必证明)，并求函数y＝f(x)的在[0，b]上单调递增区间．

     

     

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f(x)的导函数为f ′(x)，且对任意x＞0，都有f ′(x)＞．

    （Ⅰ）判断函数F(x)＝在(0，＋∞)上的单调性；

    （Ⅱ）设x1，x2∈(0，＋∞)，证明：f(x1)＋f(x2)＜f(x1＋x2)；

    （Ⅲ）请将（Ⅱ）中的结论推广到一般形式，并证明你所推广的结论．

    查看答案和解析>>

    科目：高中数学 来源：江西省南昌市2011-2012学年高三下学期第一次模拟测试卷（数学理） 题型：解答题

     

    已知向量p＝(－cos 2x，a)，q＝(a,2－sin 2x)，函数f(x)＝p·q－5(a∈R，a≠0)

    (1)求函数f(x)(x∈R)的值域；

    (2)当a＝2时，若对任意的t∈R，函数y＝f(x)，x∈(t，t＋b]的图像与直线y＝－1有且仅有两个不同的交点，试确定b的值(不必证明)，并求函数y＝f(x)的在[0，b]上单调递增区间．

     

     

     

    查看答案和解析>>

    同步练习册答案