Question

已知F₁、F₂分别是椭圆（a＞b＞0）的左、右焦点，M、N分别是直线（m是大于零的常数）与x轴、y轴的交点，线段MN的中点P在椭圆C上．
（Ⅰ）求常数m的值；
（Ⅱ）试探究直线l与椭圆C是否还存在异于点P的其它公共点？请说明理由；
（Ⅲ）当a=2时，试求△PF₁F₂面积的最大值，并求△PF₁F₂面积取得最大值时椭圆C的方程．

Answer 1

解：（Ⅰ）由已知可得M（ma，0）、N（0，mb），
故MN的中点为，
又点P在椭圆C上，∴，所以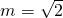

（Ⅱ）（解法一）由（Ⅰ）得，
与方程C联立得：，
即，
由于，
∴此方程有两个相等实根，
故直线l与椭圆C相切，切点为，
除此之外，不存在其他公共点

（解法二）由（Ⅰ）得，与方程C联立得：
所以，则
∴和是方程的两根，
又，∴此方程有两个相等实根，即，
∴直线l与椭圆C的公共点是唯一的点，
即除点P以外，不存在其他公共点

（Ⅲ）当a=2时，=，
所以，
当且仅当时，等式成立，故
此时，椭圆C的方程为：

分析：（Ⅰ）由已知可得M（ma，0）、N（0，mb），从而可得MN的中点为P的坐标，利用点P在椭圆C上，即可求常数m的值；
（Ⅱ）（解法一）由（Ⅰ）得，与方程C联立消元，由此可得直线l与椭圆C相切时切点的坐标；
（解法二）由（Ⅰ）得，与方程C联立，可得，从而和是方程的两根，由此可得直线l与椭圆C的公共点是唯一的点P；
（Ⅲ）当a=2时，表示△PF₁F₂面积，利用基本不等式，可求△PF₁F₂面积的最大值，从而可得椭圆C的方程．
点评：本题考查直线与椭圆的位置关系，考查三角形面积的计算，考查基本不等式的运用，联立直线与椭圆方程是关键．