Question

对于定义域为[0，1]的函数f（x），若同时满足以下三个条件：
①f（1）=1； 
②x∈[0，1]，总有f（x）≥0；
③当x₁≥0，x₂≥0，x₁+x₂≤1时，都有f（x₁+x₂）≥f（x₁）+f（x₂），则称函数f（x）为理想函数．
（Ⅰ）若函数f（x）为理想函数，求f（0）．
（Ⅱ）判断函数g（x）=2x﹣1（x∈[0，1]）和函数 （x∈[0，1]）是否为理想函数？若是，予以证明；若不是，说明理由．
（Ⅲ）设函数f（x）为理想函数，若x₀∈[0，1]，使f（x₀）∈[0，1]，且f[f（x₀）]=x₀，求证：f（x₀）=x₀．

Answer 1

解：（Ⅰ）取x₁=x₂=0，代入f（x₁+x₂）≥f（x₁）+f（x₂），
可得f（0）≥f（0）+f（0）即f（0）≤0
由已知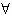x∈[0，1]，总有f（x）≥0可得f（0）≥0，
∴f（0）=0
（Ⅱ）显然g（x）=2^x﹣1在[0，1]上满足g（x）≥0；
②g（1）=1．若x₁≥0，x₂≥0，且x₁+x₂≤1，则有
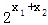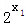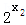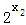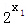g（x₁+x₂）﹣[g（x₁）+g（x₂）]= ﹣1﹣[（ ﹣1）+（ ﹣1）]=（ ﹣1）（ ﹣1）≥0
故g（x）=2^x﹣1满足条件①②③，
所以g（x）=2^x﹣1为理想函数．对应函数 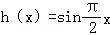在x∈[0，1]上满足
①h（1）=1； 
②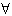x∈[0，1]，总有h（x）≥0； 
③但当x₁≥0，x₂≥0，x₁+x₂≤1时，例如 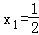=x₂时，h（x₁+x₂）=h（1）=1，
而h（x₁）+h（x₂）=2h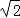（ ）= ，不满足条件③，则函数h（x）不是理想函数．
（Ⅲ）由条件③知，任给m、n∈[0，1]，当m＜n时，由m＜n知n﹣m∈[0，1]，
∴f（n）=f（n﹣m+m）≥f（n﹣m）+f（m）≥f（m）．
若f（x₀）＞x₀，则f（x₀）≤f[f（x₀）]=x₀，前后矛盾；
若f（x₀）＜x₀，则f（x₀）≥f[f（x₀）]=x₀，前后矛盾．
故f（x₀）=x₀．