练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    若G是△ABC的重心,D,E,F分别是AB,BC,CA的中点,则++等于（    ）

    A.6           B.-6            C.-6           D.0

    解析:在图中,令GB的中点为P,连结DP,PE,得平行四边形GDPE.

    取向量,为一组基底,则有

    =2=2(+),

    =-2,=-2.

    上面三式两端相加,有++=0.

    ∴应选D.

    答案:D

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    设P是△ABC内任意一点，S△ABC表示△ABC的面积，λ1=
    S△PBC
    S△ABc
    ，λ2=
    S△PCA
    S△ABC
    ，λ3=
    S△PAB
    S△ABC
    ，定义f（P）=（λ1，λ2，λ3），若G是△ABC的重心，f（Q）=（
    1
    2
    ，
    1
    3
    ，
    1
    6
    ），则（　　）
    A、点Q在△GAB内
    B、点Q在△GBC内
    C、点Q在△GCA内
    D、点Q与点G重合

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设P是△ABC内任意一点,S△ABC表示△ABC的面积,λ1=,λ2=,λ3=,定义f(P)=(λ1,λ2,λ3),若G是△ABC的重心,f(Q)=(, , ),则(   )

    A.点Q在△GAB内                           B.点Q在△GBC内

    C.点Q在△GCA内                           D.点Q与点G重合

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设P是△ABC内任意一点，S△ABC表示△ABC的面积，λ1= ，λ2=,λ3=，定义f（P）=（λ1，λ2，λ3）.若G是△ABC的重心，f（Q）=（,，），则（    ）

    A.点Q在△GAB内                                   B.点Q在△GBC内

    C.点Q在△GCA内                                   D.点Q与G重合

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设P是△APC内任意一点，S△ABC表示△ABC的面积，λ1＝，λ2＝，λ3＝，定义

    f(P)=( λ1, λ2, λ3),若G是△ABC的重心，f(Q)＝（，，），则

    A、点Q在△GAB内               B、点Q在△GBC内　

    C、点Q在△GCA内　             D、点Q与点G重合

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年河北省高三上学期期末考试文科数学 题型：选择题

    设P是△ABC内任意一点，S△ABC表示△ABC的面积，λ1＝， λ2＝，λ3＝，定义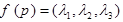,若G是△ABC的重心，f（Q）＝（，，），则

    A．点Q在△GAB内　                  B．点Q在△GBC内

    C．点Q在△GCA内　                  D．点Q与点G重合

                             第Ⅱ卷（共90分）

     

    查看答案和解析>>

    同步练习册答案