Question

在△ABC中，h_a,h_b,h_c为边长a,b,c上的高，求证：asinA+bsinB+csinC≥h_a+h_b+h_c.

Answer 1

思路分析：解题关键是将h_a，h_b，h_c结合已知量转化为积的形式，进而运用排序原理去求证.

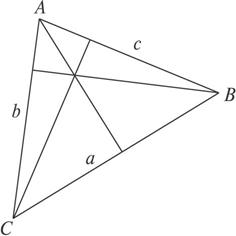
证明：如下图,h_a=bsinC;h_b=csinA,h_c=asinB,不妨设a≥b≥c;由大角对大边可知A≥B≥C.

①若A≤90°，则有sinA≥sinB≥sinC,由顺序和≥乱序和，可得asinA+bsinB+csinC≥asinB+bsinC+csinA.

②若A＞90°,此时,sinA=sin(B+C),因为B+C为锐角,故亦有sinA≥sinB≥sinC.由顺序和≥乱序和，可得asinA+bsinB+csinC≥asinB+bsinC+csinA.

综上可知,asinA+bsinB+csinC≥h_a+h_b+h_c成立.

巧妙变式

    用A、B、C表示△ABC的三内角的弧度数，a、b、c表示其对边，求证≥.

证明：由对称性，不妨设a≥b≥c,于是A≥B≥C，于是由顺序和≥乱序和，可得

aA+bB+cC=aA+bB+cC,

aA+bB+cC≥aB+bC+cA,

aA+bB+cC≥aC+bA+cB.

将上面三式相加可得

3（aA+bB+cC）≥(a+b+c)(A+B+C)=π(a+b+c).

因为a+b+c＞0，所以≥.