练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    数列｛an｝中，an=2n+1，那么a2n为(    )

    A.2n+1              B.4n+1              C.4n+2            D.4n

    提示：有了通项公式，求第几项只要把项数代入即可.因为a2n=2（2n）+1=4n+1，故选B.

    答案：B

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    关于数列有下列四个判断：
    ①若a，b，c，d成等比数列，则a+b，b+c，c+d也成等比数列；
    ②若数列{an}是等比数列，则Sn，S2n-Sn，S3n-S2n…也成等比数列；
    ③若数列{an}既是等差数列也是等比数列，则{an}为常数列；
    ④数列{an}的前n项的和为Sn，且Sn=an-1(a∈R)，则{an}为等差或等比数列；
    ⑤数列{an}为等差数列，且公差不为零，则数列{an}中不会有am=an（m≠n）．
    其中正确命题的序号是
    ②③④⑤
    ②③④⑤
    ．（请将正确命题的序号都填上）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•徐汇区一模）对于数列{xn}，从中选取若干项，不改变它们在原来数列中的先后次序，得到的数列称为是原来数列的一个子数列．某同学在学习了这一个概念之后，打算研究首项为正整数a，公比为正整数q（q＞0）的无穷等比数列{an}的子数列问题．为此，他任取了其中三项ak，am，an（k＜m＜n）．
    （1）若ak，am，an（k＜m＜n）成等比数列，求k，m，n之间满足的等量关系；
    （2）他猜想：“在上述数列{an}中存在一个子数列{bn}是等差数列”，为此，他研究了ak+an与2am的大小关系，请你根据该同学的研究结果来判断上述猜想是否正确；
    （3）他又想：在首项为正整数a，公差为正整数d的无穷等差数列中是否存在成等比数列的子数列？请你就此问题写出一个正确命题，并加以证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•上海）在数列（an）中，an=2n-1，若一个7行12列的矩阵的第i行第j列的元素cij=ai•aj+ai+aj（i=1，2，…，7；j=1，2，…，12），则该矩阵元素能取到的不同数值的个数为（　　）

    查看答案和解析>>

    科目：高中数学 来源：高考零距离　二轮冲刺优化讲练　数学 题型：022

    关于数列有下面四个命题：

    ①若a，b，c，d成等比数列，则a＋b，b＋c，c＋d也成等比数列；

    ②若数列｛an｝既是等差数列也是等比数列，则｛an｝为常数列；

    ③若数列｛an｝的前n项和为Sn，且Sn＝an－1(a∈R)，则｛an｝为等差或等比数列；

    ④若数列｛an｝为等差数列，且公差不为零，则数列｛an｝中不会有am＝an(m≠n)．

    其中正确命题的序号是________(注：把你认为是正确命题的序号都填上)．

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年浙江省高三12月阶段性检测理科数学试卷 题型：解答题

    将数列｛an｝中的所有项按每一行比上一行多一项的规则排成如下数表：

    a1

    a2  a3

    a4   a5  a6

    a7  a8   a9    a10

    ……

    记表中的第一列数a1，a2，a4，a7，…构成的数列为｛bn｝,b1=a1=1. Sn为数列｛bn｝的前n项和，且满足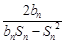=1（n≥2）.

    (Ⅰ)证明数列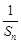｛｝成等差数列，并求数列｛bn｝的通项公式；

    （Ⅱ）上表中，若从第三行起，每一行中的数按从左到右的顺序均构成等比数列，且公比为同一个正数.当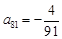时，求上表中第k(k≥3)行所有项的和．

     

    查看答案和解析>>

    同步练习册答案