Question

a为何值时，方程sin²x+2sinxcosx－2cos²x=a有实数解.

Answer 1

a∈［，］

解析:

分析:所给方程的特征较明显，即是关于sinx与cosx的齐次方程，通过变形就可化为以tanx为变元的一元二次方程，从而据判别式进行求解.

解法一:原方程可化为

sin²x+2sinxcosx－2cos²x=a（sin²x+cos²x），

即（1－a）sin²x+2sinxcosx－（2+a）cos²x=0.

（1）当a≠1时，∵cosx≠0，∴方程两边同除以cos²x，得

（1－a）tan²x+2tanx－（2+a）=0.

∵tanx∈R，∴Δ≥0，即4+4（1－a）（2+a）≥0，

即a²+a－3≤0.又a≠1，

∴a∈［，1）∪（1，］.

（2）当a=1时，原方程化为2sinxcosx－3cos²x=0，此方程有实根.

综合（1）（2）可得当a∈［，］时，原方程有实数根.

解法二:（用函数观点）

当实数a取函数y=sin²x+2sinxcosx－2cos²x值域中的数值时，原方程有实根.因此，求a的范围，实质上就是求上述函数的值域.

∵y=sin²x+2sinxcosx－2cos²x

=1+sin2x－3cos²x

=1+sin2x－ （1+cos2x）

=sin2x－cos2x－=sin（2x－）－，

其中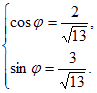∴y∈［， ］，

即a∈［，］时，原方程有实数根.

评注: 解法一是常规解法，解法二利用了变换的观点，通过函数思想来解方程.函数与方程是数学中两个重要的概念，在解决数学问题时，如能灵活运用，将使解答具有创造性.