
(Ⅰ)求AD边所在直线的方程;
(Ⅱ)求矩形ABCD外接圆的方程;
(Ⅲ)若动圆P过点N(-2,0),且与矩形ABCD的外接圆外切,求动圆P的圆心的轨迹方程.
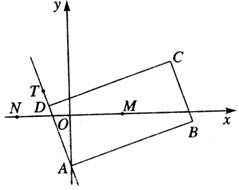
解:(Ⅰ)因为AB边所在直线的方程为x-3y-6=0,且AD与AB垂直,所以直线AD的斜率为-3.
又因为点T(-1,1)在直线AD上,
所以AD边所在直线的方程为y-1= -3(x+1),
即3x+y+2=0.
(Ⅱ)由![]() 解得点A的坐标为(0,-2).
解得点A的坐标为(0,-2).
因为矩形ABCD两条对角线的交点为M(2,0),
所以M为矩形ABCD外接圆的圆心.
又|AM|=![]() =2
=2![]() ,
,
从而矩形ABCD外接圆的方程为(x-2)2+y2=8.
(Ⅲ)因为动圆P过点N,所以|PN|是该圆的半径,又因为动圆P与圆M外切,
所以| PM |=| PN |+2![]() ,
,
即| PM | - | PN |=2![]() .
.
故点P的轨迹是以M,N为焦点,实轴长为2![]() 的双曲线的左支.
的双曲线的左支.
因为实半轴长a=![]() ,半焦距c=2,
,半焦距c=2,
所以虚半轴长b=![]() =
=![]() .
.
从而动圆P的圆心的轨迹方程为![]() =1(x≤ -
=1(x≤ -![]() ).
).


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:
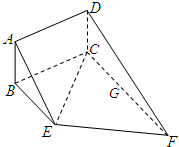 如图,矩形ABCD和梯形BEFC所在的平面互相垂直,BE∥CF,∠BCF=∠CEF=
如图,矩形ABCD和梯形BEFC所在的平面互相垂直,BE∥CF,∠BCF=∠CEF=| π |
| 2 |
| 3 |
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•湛江一模)如图,矩形ABCD中,AB=2BC=4,E为边AB的中点,将△ADE沿直线DE翻折成△A1DE
(2013•湛江一模)如图,矩形ABCD中,AB=2BC=4,E为边AB的中点,将△ADE沿直线DE翻折成△A1DE查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com