Question

已知△ABC所在平面与直角梯形ACEF所在平面垂直,AF⊥AC,EB⊥AB,AF∥CE,AB=BC=CE=2AF=2,O为AC中点.

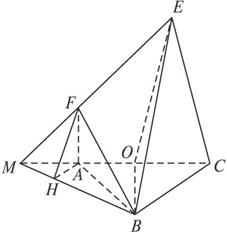
(1)求证:面OBE⊥面ACEF;

(2)求面EFB与面ABC所成二面角的大小.

Answer 1

(1)证明:在△ABC中,AB=BC,O为AC中点,

∴OB⊥AC.

∵平面ABC⊥平面ACEF,且平面ABC∩平面ACEF=AC,OB平面ABC,

∴OB⊥平面ACEF.又OB面OBE,

∴面OBE⊥面ACEF.

(2)解:延长EF交CA的延长线于点M,连结BM,

则面EFB∩面ABC=BM.

作AH⊥BM于点H,连结FH,

∵平面ABC⊥平面ACEF,

且平面ABC∩平面ACEF=AC,AF⊥AC,

∴AF⊥平面ABC.

由三垂线定理得FH⊥BM,

因此,∠FAH为面EFB与面ABC所成二面角的平面角.

∵AF∥CE,AF⊥平面ABC,

∴CE⊥平面ABC.

又EB⊥AB,由三垂线定理的逆定理得BC⊥AB,

∵AF=1,且A为CM中点,

在△MBO中,MO=3,OB=,

∴MB==2.

又Rt△MAH∽Rt△MBO,

∴,

即AH=.

在△FAH中,tan∠FHA=,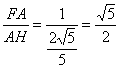

面EFB与面ABC所成二面角的大小为arctan.