
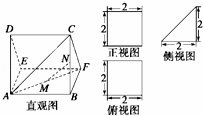
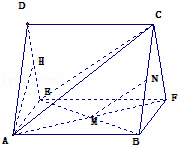
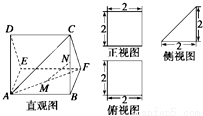
如图,多面体AEDBFC的直观图及三视图如图所示,M,N分别为AF,BC的中点.
(1)求证:MN∥平面CDEF;
(2)求多面体A﹣CDEF的体积.
考点:
直线与平面平行的判定;由三视图还原实物图;棱柱、棱锥、棱台的体积.
专题:
计算题;证明题.
分析:
(1)通过三视图说明几何体的特征,证明MN平行平面CDEF内的直线BC,即可证明MN∥平面CDEF;
(2)说明四边形 CDEF是矩形,AH⊥平面CDEF,然后就是求多面体A﹣CDEF的体积.
解答:
解:(1)证明:由多面体AEDBFC的三视图知,三棱柱AED﹣BFC中,底面DAE是等腰
直角三角形,DA=AE=2,DA⊥平面ABEF,侧面ABFE,ABCD都是边长为2的正方形.
连接EB,则M是EB的中点,
在△EBC中,MN∥EC,
且EC⊂平面CDEF,MN⊄平面CDEF,
∴MN∥平面CDEF.
(2)因为DA⊥平面ABEF,EF⊂平面ABEF,∴EF⊥AD,
又EF⊥AE,所以,EF⊥平面ADE,
∴四边形 CDEF是矩形,
且侧面CDEF⊥平面DAE
取DE的中点H,∵DA⊥AE,DA=AE=2,∴![]() ,
,
且AH⊥平面CDEF.
所以多面体A﹣CDEF的体积![]() .
.
点评:
本题是中档题,考查直线与平面平行的证明方法,几何体的体积的求法,考查计算能力.


科目:高中数学 来源: 题型:
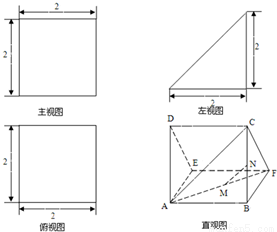
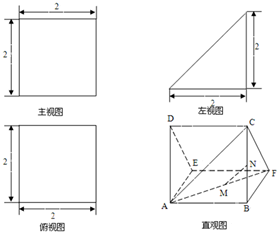 如图,多面体AEDBFC的直观图及三视图如图所示,M,N分别为AF,BC的中点.
如图,多面体AEDBFC的直观图及三视图如图所示,M,N分别为AF,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
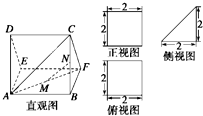 (2010•汕头模拟)如图,多面体AEDBFC的直观图及三视图如图所示,M,N分别为AF,BC的中点.
(2010•汕头模拟)如图,多面体AEDBFC的直观图及三视图如图所示,M,N分别为AF,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,多面体AEDBFC的直观图及三视图如图所示,M,N分别为AF,BC的中点.
如图,多面体AEDBFC的直观图及三视图如图所示,M,N分别为AF,BC的中点.查看答案和解析>>
科目:高中数学 来源:2010年广东省汕头市重点中学高三联考数学试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2010年高考数学猜题精粹(文科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com