练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    某厂要生产甲、乙两种产品,甲产品每单位需A种原料8 g,B种原料24 g,每单位利润60元;乙产品每单位需A种原料16 g,B种原料16 g,每单位利润80元.现A种原料库存量为2 400 g,B种原料库存量为2 880 g.问甲、乙两种产品各生产多少单位,工厂可获得最大利润?(原料不再外购,产品可完全售出)

    解析:设生产甲、乙两种产品分别为x单位、y单位,所获利润为z元,依题意有

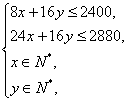    z=60x+80y.

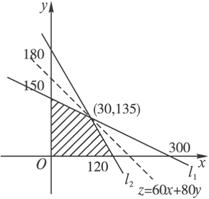
    分别作出直线l1:8x+16y=2 400,l2:24x+16y=2 880.

    画出8x+16y≤2 400,24x+16y≤2 800以及x＞0,y＞0

    在平面上表示的区域,如图所示.

    由解得交点为M(30,135).

    再由z=60x+80y,知y=-x+.

    ∴z的最大值即由直线y=-x+在y轴上的截距的最大值确定,在上图的可行域内,其过点M(30,135)时,z最大.

    ∴zmax=60×30+80×135=12 600(元).

    故当工厂生产甲产品30单位,生产乙产品135单位时,可获得最大利润.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    某厂生产甲产品每千克需用原料A和原料B分别为a1、b1千克，生产乙产品每千克需用原料A和原料B分别为a2、b2千克．甲、乙产品每千克可获利润分别为d1、d2元．月初一次性购进本月用原料A、B各c1、c2千克．要计划本月生产甲、乙两种产品各多少千克才能使月利润总额达到最大．在这个问题中，设全月生产甲、乙两种产品分别为x千克、y千克，月利润总额为z元，那么，用于求使总利润z=d1x+d2y最大的数学模型中，约束条件为（　　）
    A、
    a1x+a2y≥c1
    b1x+b2y≥c2
    x≥0
    y≥0
    B、
    a1x+b1y≤c1
    a2x+b2y≤c2
    x≥0
    y≥0
    C、
    a1x+a2y≤c1
    b1x+b2y≤c2
    x≥0
    y≥0
    D、
    a1x+a2y=c1
    b1x+b2y=c2
    x≥0
    y≥0

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某厂要生产甲种产品45个，乙种产品55个，所用原料为A、B两种规格的金属板，其面积分别为2m2和3m2，用A种可同时造甲种产品3个和乙种产品5个，用B种可同时造甲、乙两种产品各6个．问A、B两种原料各取多少块可保证完成任务，且使总的用料（面积）最小？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某厂拟生产甲、乙两种适销产品，每件利润分别为300、500元，甲、乙产品的部件各自在A、B两个车间分别生产，每件甲、乙产品的部件分别需要A、B车间的生产能力1、2工时；两种产品的部件最后都要在C车间装配，装配每件甲、乙产品分别需要3、4工时.A、B、C三个车间每天可用于生产这两种产品的工时分别为8、12、36，应如何安排生产这两种产品才能获利最多？

    查看答案和解析>>

    科目：高中数学 来源：2010年高考试题分项版理科数学之专题十一概率统计 题型：解答题

    （10分）某厂生产甲、乙两种产品，生产甲产品一等品80%，二等品20%；生产乙产品，一等品90%，二等品10%。生产一件甲产品，如果是一等品可获利4万元，若是二等品则要亏损1万元；生产一件乙产品，如果是一等品可获利6万元，若是二等品则要亏损2万元。设生产各种产品相互独立

    （1）记x（单位：万元）为生产1件甲产品和件乙产品可获得的总利润，求x的分布列

    （2）求生产4件甲产品所获得的利润不少于10万元的概率

     

    查看答案和解析>>

    同步练习册答案