
本题有2小题,第1小题6分,第2小题10分.
|
 到定直线
到定直线 的距离
的距离 ,
, 为该平面上的动点,过
为该平面上的动点,过 作直线
作直线 的垂线,垂足为
的垂线,垂足为 ,且
,且 .
.
(1)试建立适当的平面直角坐标系,求动点 的轨迹
的轨迹 的方程;
的方程;
(2)过点 的直线交轨迹
的直线交轨迹 于
于 、
、 两点,交直线
两点,交直线 于点
于点 ,
,
已知 ,
, ,求证:
,求证: 为定值.
为定值.
(1)方法一:如图,以线段 的中点为原点
的中点为原点 ,
,
|
 所在的直线为
所在的直线为 轴建立直角坐标系
轴建立直角坐标系 .
.
则, . ……………………………2分
. ……………………………2分
设动点 的坐标为
的坐标为 ,则动点
,则动点 的坐标为
的坐标为
 ,
, , …………2分
, …………2分
由 ,得
,得 ,…2分
,…2分
方法二:由 得,
得, .…………………………2分
.…………………………2分
所以,动点 的轨迹
的轨迹 是抛物线,以线段
是抛物线,以线段 的中点
的中点
为原点 ,以线段
,以线段 所在的直线为
所在的直线为 轴建立直角坐标系
轴建立直角坐标系 ,可得轨迹
,可得轨迹 的方程为:
的方程为: .…………………………………………………………4分
.…………………………………………………………4分
(2)方法一:如图,设直线 的方程为
的方程为 ,
, ,
, ,……1分
,……1分
则 .
……………………………………………………………………………1分
.
……………………………………………………………………………1分
联立方程组 消去
消去 得,
得,
 ,
, ,故 …………………………………………1分
,故 …………………………………………1分
 ……………………………………………………………………………1分
……………………………………………………………………………1分
由 ,
, 得,
得,
 ,
, ,……………………………………………………2分
,……………………………………………………2分
整理得, ,
, ,
,
 .…………………4分
.…………………4分
方法二:由已知 ,
, ,得
,得 . …………………2分
. …………………2分
于是, , ① …………………………………………………3分
, ① …………………………………………………3分
如图,过 、
、 两点分别作准线
两点分别作准线 的垂线,垂足分别为
的垂线,垂足分别为 、
、 ,
,
则有 ② …………………………………………………3分
② …………………………………………………3分
由①,②得 .…………………………………………………………………2分
.…………………………………………………………………2分


科目:高中数学 来源: 题型:
(满分14分)本题有2小题,第1小题6分,第2小题8分.
已知在平面直角坐标系![]() 中,
中,![]() 三个顶点的直角坐标分别为
三个顶点的直角坐标分别为![]() ,
,![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() 为锐角三角形,求
为锐角三角形,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
(满分14分)本题有2小题,第1小题7分,第2小题7分.
已知在平面直角坐标系![]() 中,
中,![]() 三个顶点的直角坐标分别为
三个顶点的直角坐标分别为![]() ,
,![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() 为钝角,求
为钝角,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2011届上海市闸北区高三第一学期期末数学理卷 题型:解答题
(满分20分)本题有2小题,第1小题12分,第2小题8分.
已知数列{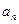 }和{
}和{ }满足:对于任何
}满足:对于任何 ,有
,有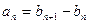 ,
, 为非零常数),且
为非零常数),且 .
.
(1)求数列{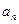 }和{
}和{ }的通项公式;
}的通项公式;
(2)若 是
是 与
与 的等差中项,试求
的等差中项,试求 的值,并研究:对任意的
的值,并研究:对任意的 ,
, 是否一定能是数列{
是否一定能是数列{ }中某两项(不同于
}中某两项(不同于 )的等差中项,并证明你的结论.
)的等差中项,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年上海市闸北区高三第一学期期末数学理卷 题型:解答题
(满分20分)本题有2小题,第1小题12分,第2小题8分.
已知数列{ }和{
}和{ }满足:对于任何
}满足:对于任何 ,有
,有 ,
, 为非零常数),且
为非零常数),且 .
.
(1)求数列{ }和{
}和{ }的通项公式;
}的通项公式;
(2)若 是
是 与
与 的等差中项,试求
的等差中项,试求 的值,并研究:对任意的
的值,并研究:对任意的 ,
, 是否一定能是数列{
是否一定能是数列{ }中某两项(不同于
}中某两项(不同于 )的等差中项,并证明你的结论.
)的等差中项,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年上海市闸北区高三第一学期期末数学理卷 题型:解答题
(满分15分)本题有2小题,第1小题6分,第2小题9分.
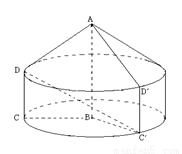
如图,在直角梯形 中,
中, ,
, ,
, ,
, .将
.将 (及其内部)绕
(及其内部)绕 所在的直线旋转一周,形成一个几何体.
所在的直线旋转一周,形成一个几何体.
(1)求该几何体的体积 ;
;

 (2)设直角梯形
(2)设直角梯形 绕底边
绕底边 所在的直线旋转角
所在的直线旋转角 (
( )至
)至 ,问:是否存在
,问:是否存在 ,使得
,使得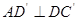 .若存在,求角
.若存在,求角 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com