练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知圆经过极点O，与极轴交于A(2a，0)点，求圆的极坐标方程．

    答案：略
    解析：

    解：设M(ρ，θ)为圆上除A(2a，0)外的任意一点，连结OM，AM，在三角形AOM中，我们有|OA|=2a，|OM|=ρ，∠AOM=θ，∠AMO=90°，故△AOM为直角三角形．所以有|OA|cosθ=|OM|，即2acosθ=ρ．

    所以，所求的圆的极坐标方程为ρ=2acosθ．

    可以验证点，(2a，0)也满足ρ=2acosθ，即A(2a，0)和极点O也在这个圆上．


    提示：

    分析：如图所示，设M(ρ，θ)为圆上任意一点，连OM、MA得直角三角形AOM，由于|OM|=ρ．|OA|=2a，∠AOM=θ，∠AMO=90°，因而在直角三角形AOM中，由已知可以求出OM，即ρ与θ的关系．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知圆C的参数方程为
    x=
    		3
    +2cosθ
    y=2sinθ
    （θ为参数），
    （1）以原点O为极点、x轴的正半轴为极轴建立极坐标系，写出圆C的极坐标方程；
    （2）已知直线l经过原点O，倾斜角α=
    π
    6
    ，设l与圆C相交于A、B两点，求O到A、B两点的距离之积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    选做题（请考生在三个小题中任选一题作答，如果多做，则按所做的第一题评阅记分）
    （A）（坐标系与参数方程选做题）在直角坐标系x0y中，以原点为极点，x轴非负半轴为极轴建立极坐标系，已知圆C与直线l的方程分别为：ρ=2sinθ，
    x=x0+
    		2
    t
    y=
    		2
    t
    （t为参数）．若圆C被直线l平分，则实数x0的值为
    -1
    -1
    ．
    （B）（不等式选做题）若关于x的不等式|x-m|＜2成立的充分不必要条件是2≤x≤3，则实数m的取值范围是
    （1，4）
    （1，4）
    ．
    （C） （几何证明选讲） 如图，割线PBC经过圆心O，OB=PB=1，OB绕点O逆时针旋转120°到OD，连PD交圆O于点E，则PE=
    3
    		7
    7
    3
    		7
    7
    ．

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年福建省泉州市安溪县高三期末质量检测数学试卷（解析版） 题型：解答题

    以直角坐标系的原点O为极点，x轴的正半轴为极轴，且两个坐标系取相等的单位长度．已知直线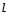经过点P(1,1),倾斜角．

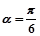    （1）写出直线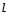的参数方程；

    （2）设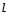与圆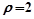相交于两点A、B，求点P到A、B两点的距离之积．

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年山东省高三上学期期末理科数学试卷 题型：解答题

    选修4—4：坐标系与参数方程

    以直角坐标系的原点O为极点，x轴的正半轴为极轴，且两个坐标系取相等的单位长度．已知直线经过点P(1,1),倾斜角．

    （1）写出直线的参数方程；

    （2）设与圆相交于两点A、B，求点P到A、B两点的距离之积．

     

    查看答案和解析>>

    同步练习册答案