分析:(I)利用线面平行的判定定理证明BD1∥平面ACM;
(Ⅱ)利用线面垂直的判定定理证明B1O⊥平面ACM;
(Ⅲ)利用锥体的体积公式求体积.
解答:解:
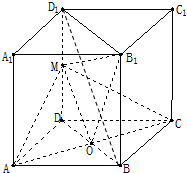
(I)证明:
连结BD,设BD与AC的交点为O,
∵AC,BD为正方形的对角线,故O为BD中点;
连结MO,
∵O,M分别为DB,DD
1的中点,
∴OM∥BD
1,…(2分)
∵OM?平面ACM,BD
1?平面ACM…(3分)
∴BD
1∥平面ACM. …(4分)
(II)∵AC⊥BD,DD
1⊥平面ABCD,且AC?平面ABCD,
∴AC⊥DD
1;且BD∩DD
1=D,∴AC⊥平面BDD
1B
1…(6分)
OB
1?平面BDD
1B
1,∴B
1O⊥AC,…(7分)
连结B
1M,在△B
1MO中,
MO2=12+()2=3,
B1O2=22+()2=6,
B1M2=12+(2)2=9,
∴
B1M2=MO2+B1O2,
∴B
1O⊥OM…(10分)
又OM∩AC=O,∴B
1O⊥平面AMC; …(11分)
法二:∵
==,∠ODM=∠B
1BO=90°,
∴△MDO∽△OBB
1,
∴∠MOD=∠OB
1B,∠MOD+∠B
1OB=90°,
∴B
1O⊥OM.
(Ⅲ)可证AO⊥平面OB
1M,则
VO-AB1M=VA-OB1M=×AO×S△OB1M=×××OB1×OM=××××=1.
点评:本题主要考查直线和平面平行或垂直的判定,以及锥体的条件公式,要求熟练掌握相应的判定定理.

 (2007•汕头二模)在正方体ABCD-A1B1C1D1中,M为DD1的中点,O为AC的中点,AB=2.
(2007•汕头二模)在正方体ABCD-A1B1C1D1中,M为DD1的中点,O为AC的中点,AB=2. (I)证明:
(I)证明:

 阅读快车系列答案
阅读快车系列答案 (2007•汕头二模)如图,要计算西湖岸边两景点B与C的距离,由于地形的限制,需要在岸上选取A和D两点,现测得AD⊥CD,AD=10km,AB=14km,∠BDA=60°,∠BCD=135°,求两景点B与C的距离(精确到0.1km).
(2007•汕头二模)如图,要计算西湖岸边两景点B与C的距离,由于地形的限制,需要在岸上选取A和D两点,现测得AD⊥CD,AD=10km,AB=14km,∠BDA=60°,∠BCD=135°,求两景点B与C的距离(精确到0.1km).