分析:法一:(1)由AB
C
1D
1,BE
D
1F,且平面ABE∥平面C
1D
1F,∠ABE=∠C
1D
1F=
,知△ABE≌△C
1D
1F,由此能够证明A、E、C
1、F四点共面.
(2)延长C
1E,CB交于G,连接AG,过B作BH⊥AG于H,连接EH,由正四棱柱ABCD-A
1B
1C
1D
1,得EB⊥平面ABCD,故EH⊥AG,所以∠EHB是所求的二面角的平面角,由此能求出平面AEC
1F与底面ABCD所成的锐二面角的大小.
(法二)(1)以C为原点,CD为x轴,CB为y轴,CC
1为z轴建立空间直角坐标系,则C
1(0,0,3),F(1,0,2),A(1,,1,0),E(0,1,1),由此能证明A、E、C
1、F四点共面.
(2)设面EC
1FA的一个法向量为
=(x,y,z),
=(0,1,-2),由
,得
=(1,2,1),又面ABCD的一个法向量为
=(0,0,1),由向量法能够求出平面AEC
1F与底面ABCD所成的锐二面角的大小.
解答: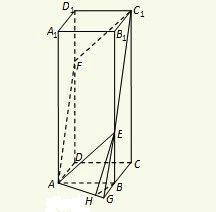
(法一)(1)证:∵AB
C
1D
1,BE
D
1F,且平面ABE∥平面C
1D
1F,
∠ABE=∠C
1D
1F=
,
∴△ABE≌△C
1D
1F,…(3分)
∴
AEC1F,∴A、E、C
1、F四点共面.…(6分)
(2)延长C
1E,CB交于G,连接AG,过B作BH⊥AG于H,连接EH,
由正四棱柱ABCD-A
1B
1C
1D
1,得EB⊥平面ABCD,∴EH⊥AG,
∴∠EHB是所求的二面角的平面角,…(9分)
由△GBE∽△GCC
1得
==
,∴GB=
,在Rt△ABG中,
AG=
,BH=
=
,
∴tan∠EHB=
=
,…(11分)
所以平面AEC
1F与底面ABCD所成的锐二面角的大小为arctan
.…(12分)
(法二)(1)以C为原点,CD为x轴,CB为y轴,CC
1为z轴建立如图所示的空
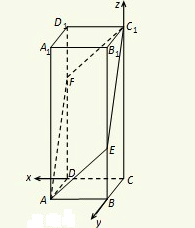
间直角坐标系,则C
1(0,0,3),F(1,0,2),A(1,,1,0),E(0,1,1),…(2分)
∴
=(1,0,-1),
=(1,0,-1),
∴C
1F∥EA,∴A、E、C
1、F四点共面.…(6分)
(2)设面EC
1FA的一个法向量为
=(x,y,z),∵
=(0,1,-2),
由
,得
=(1,2,1),
又面ABCD的一个法向量为
=(0,0,1),…(9分)
∴cos<
,>=
=
=
,…(11分)
所以平面AEC
1F与底面ABCD所成的锐二面角的大小为arccos
.(12分)
点评:本题考查四点共面的证明,考查二面角的求法,解题时要认真审题,注意合理地化空间几何为平面几何进行求解,解题时要注意向量法的合理运用.

 如图,正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=3,E、F分别在侧棱BB1、DD1上,且BE=1,D1F=1.
如图,正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=3,E、F分别在侧棱BB1、DD1上,且BE=1,D1F=1. (法一)(1)证:∵AB
(法一)(1)证:∵AB


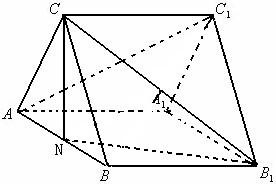 如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
 如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
