
 的值域是________.
的值域是________. )
) =
= ,根据式子的几何意义可得,转化为求一动点M(x,0)定点A(
,根据式子的几何意义可得,转化为求一动点M(x,0)定点A( )与B(
)与B( )的距离和的最值,作A(
)的距离和的最值,作A( )关于x轴对称的点C(
)关于x轴对称的点C(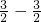 )则AM=CM,可得y=
)则AM=CM,可得y= =
= (M+BM)=
(M+BM)= (MB+MC),结合图象可知当三点共线时,MB+MC最小,代入可求答案.
(MB+MC),结合图象可知当三点共线时,MB+MC最小,代入可求答案. 解:函数y=
解:函数y= =
=
 )与B(
)与B( )的距离和的最值
)的距离和的最值 )关于x轴对称的点C(
)关于x轴对称的点C(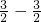 )则AM=CM,
)则AM=CM, =
=
 (M+BM)=
(M+BM)= (MB+MC)
(MB+MC) =
=




 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com