
求函数y=![]() (a>0且a≠1)的定义域.
(a>0且a≠1)的定义域.
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源:北京市育才中学2007-2008学年度高三第一次质量检测数学试题 题型:044
已知函数f(x)与函数y=![]() (a>0)的图象关于y=x对称.
(a>0)的图象关于y=x对称.
(1)求f(x);
(2)若无穷数列{an}满足a1=1,Sn=a1+a2+…+an,且点Pn(![]() ,Sn)均在函数y=f(x)上,求a的值,并求数列{
,Sn)均在函数y=f(x)上,求a的值,并求数列{![]() }的所有项的和(即前n项和的极限).
}的所有项的和(即前n项和的极限).
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省兖州市高三9月入学诊断理科数学试卷(解析版) 题型:解答题
(12分)已知函数f(x)=x3+mx2+nx-2的图象过点(-1,-6),且函数g(x)= +6x的图象关于y轴对称.
+6x的图象关于y轴对称.
(1)求m、n的值及函数y=f(x)的单调区间;(6分)
(2)若a>0,求函数y=f(x)在区间(a-1,a+1)内的极值.(6分)
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省高三预测卷2数学 题型:解答题
(本小题满分14分)
如图,某市拟在道路的一侧修建一条运动赛道,赛道的前一部分为曲线段ABC,该曲线段为函数y= (A>0,
(A>0, >0,
>0,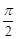 <
< <
<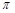 ),x∈[-3,0]的图象,且图象的最高点为B(-1,
),x∈[-3,0]的图象,且图象的最高点为B(-1,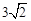 );赛道的中间部分为
);赛道的中间部分为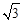 千米的水平跑到CD;赛道的后一部分为以O圆心的一段圆弧
千米的水平跑到CD;赛道的后一部分为以O圆心的一段圆弧 .
.

(1)求 ,
, 的值和∠DOE的值;
的值和∠DOE的值;
(2)若要在圆弧赛道所对应的扇形区域内建一个“矩形草坪”,如图所示,矩形的一边在道路AE上,一个顶点在扇形半径OD上.记∠POE= ,求当“矩形草坪”的面积最大时
,求当“矩形草坪”的面积最大时 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省高三预测卷2数学 题型:解答题
(本小题满分14分)
如图,某市拟在道路的一侧修建一条运动赛道,赛道的前一部分为曲线段ABC,该曲线段为函数y= (A>0,
(A>0, >0,
>0, <
< <
< ),x∈[-3,0]的图象,且图象的最高点为B(-1,
),x∈[-3,0]的图象,且图象的最高点为B(-1, );赛道的中间部分为
);赛道的中间部分为 千米的水平跑到CD;赛道的后一部分为以O圆心的一段圆弧
千米的水平跑到CD;赛道的后一部分为以O圆心的一段圆弧 .
.

(1)求 ,
, 的值和∠DOE的值;
的值和∠DOE的值;
(2)若要在圆弧赛道所对应的扇形区域内建一个“矩形草坪”,如图所示,矩形的一边在道路AE上,一个顶点在扇形半径OD上.记∠POE= ,求当“矩形草坪”的面积最大时
,求当“矩形草坪”的面积最大时 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com