

分析 (Ⅰ)由函数图象可得T,由周期公式从而可求ω,由点($\frac{π}{4}$,0)在函数图象上,结合范围0≤φ<2π,即可解得φ的值,从而得解;
(Ⅱ)由2k$π+\frac{π}{2}$≤3x+$\frac{5π}{4}$≤2k$π+\frac{3π}{2}$,k∈Z可解得函数f(x)的单调递减区间.
(Ⅲ)由x∈[0,$\frac{π}{4}$],可得3x+$\frac{5π}{4}$∈[$\frac{5π}{4}$,2π],从而可求f(x)的值域.
解答 解:(Ⅰ)由函数图象可得:$\frac{3}{2}$T=($\frac{5π}{4}-\frac{π}{4}$)=π,解得:T=$\frac{2π}{3}$=$\frac{2π}{ω}$,从而可求ω=3,
由点($\frac{π}{4}$,0)在函数图象上,
所以:2sin(3×$\frac{π}{4}$+φ)=0,
由图象可知:φ=2kπ-$\frac{3π}{4}$,k∈Z,
由0≤φ<2π,
从而可得:φ=$\frac{5π}{4}$.
故可得:f(x)=2sin(3x+$\frac{5π}{4}$).
(Ⅱ)由于f(x)=2sin(3x+$\frac{5π}{4}$),
由2k$π+\frac{π}{2}$≤3x+$\frac{5π}{4}$≤2k$π+\frac{3π}{2}$,k∈Z,
可解得函数f(x)的单调递减区间为:[$\frac{2kπ}{3}$-$\frac{π}{4}$,$\frac{2kπ}{3}+\frac{π}{12}$],k∈Z,
(Ⅲ)由于f(x)=2sin(3x+$\frac{5π}{4}$),
∵x∈[0,$\frac{π}{4}$],
∴3x+$\frac{5π}{4}$∈[$\frac{5π}{4}$,2π],
可得:f(x)=2sin(3x+$\frac{π}{4}$)∈[-2,0].
点评 本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,三角函数的图象与性质,属于基本知识的考查.


科目:高中数学 来源: 题型:解答题
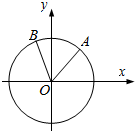 如图,在平面直角坐标系xOy中,以Ox轴为始边作角α和β,$α∈({0,\frac{π}{2}}),β∈({\frac{π}{2},π})$,其终边分别交单位圆于A,B两点.若A,B两点的横坐标分别是$\frac{3}{5}$,-$\frac{{\sqrt{2}}}{10}$. 试求
如图,在平面直角坐标系xOy中,以Ox轴为始边作角α和β,$α∈({0,\frac{π}{2}}),β∈({\frac{π}{2},π})$,其终边分别交单位圆于A,B两点.若A,B两点的横坐标分别是$\frac{3}{5}$,-$\frac{{\sqrt{2}}}{10}$. 试求查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com