练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    数学公式的值域为________，数学公式的值域为________．

    [-4，-2]    [-5，-1]
    分析：（1）是形如y=asinx+bcosx的函数模型求值域，可以化为一个三角函数的名下处理．
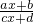    （2）是形如y=的函数模型求值域，可以想办法去掉分子的变量x，即利用反函数思想解决问题．
    解答：（1）-4=2|sin（x-）|-4，
    ∴0≤|sin（x-）|≤1，∴-4≤2|sin（x-）|-4≤-2
    故答案为：[-4，-2]．
    （2） y==4-，
    ∵-1≤cosx≤1，∴1≤cosx+2≤3，3≤≤9，
    ∴-5≤4-≤1，
    故答案为：[-5，-1]．
    点评：求函数值域的常见题型与方法：
    （1）形如y=asinx+bcosx的函数模型，宜采用化简到同一三角函数名下处理．
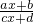    （2）形如y=的函数模型，宜采用反函数法处理．
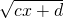    （3）形如y=（ax+b）+的函数模型，宜采用换元法处理．
    （4）复合函数模型，单调性遵循同增异减，值域需要知道构成复合的每一个函数的性质．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    对函数f（x）=
    sinx    sinx≥cosx
    cosx    sinx＜cosx
    有下列命题：
    ①f（x）的值域为[-1，1]；
    ②当且仅当x=2kл+
    π
    2
    ，k∈Z时，该函数取最大值1；
    ③f（x）是以л为最小正周期的函数； 
    ④当且仅当2kл+л＜x＜2kл+
    3π
    2
    ，k∈Z时，f（x）＜0．
    其中正确的是（　　）

    查看答案和解析>>

    科目：高中数学 来源：成功之路·突破重点线·数学（学生用书） 题型：013

    定义域为R的函数y＝f(x)的值域为[a，b]则函数y＝f(x＋a)的值域为

    [　　]

    A．[2a，a＋b]

    B．[0，b－a]

    C．[a，b]

    D．[－a，a＋b]

    查看答案和解析>>

    科目：高中数学 来源：成功之路·突破重点线·数学（学生用书） 题型：013

    已知f(x)＝3x－b(2≤x≤4，b为常数)的图象经过点(2，1)，则F(x)＝[f－1(x)]2－f－1(x2)的值域为

    [　　]

    A．[2，5]
    B．[1，＋∞)
    C．[2，10]
    D．[2，13]

    查看答案和解析>>

    科目：高中数学 来源：成功之路·突破重点线·数学（学生用书） 题型：022

    以下四个命题中：

    ①f(x＋a)＝(a≠0，x∈R)是以2a为周期的周期函数．

    ②对任何x、y∈N*，都有f(x＋y)＝f(x)＋f(y)＋xy，且f(1)＝1，则f(5)＝15．

    ③如果函数f(x)＝的反函数等于函数f(x)本身，则a＝－1．

    ④函数y＝|x＋1|＋的值域为[2，＋∞)

    其中正确的命题的序号是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设g(x)是定义在R上，以1为周期的函数，若函数f(x)＝x＋g(x)在区间[0,1]上的值域为[－2,5]，则f(x)在区间[0,3]上的值域为________．

    查看答案和解析>>

    同步练习册答案