已知函数 ,f(2)=1.
,f(2)=1.
(1)求a的值; (2)求证:函数f(x)在(-∞,0)内是减函数.
解:(1)由已知,得

,
∴a=2.…
证明:(2)由(1)得

,
设任意x
1,x
2∈(-∞,0),且x
1<x
2.
则

.…
∵x
1,x
2∈(-∞,0),且x
1<x
2.
∴x
2-x
1>0,x
1x
2>0,
∴f(x
1)-f(x
2)>0,即f(x
1)>f(x
2).
所以,函数f(x)在(-∞,0)内是减函数.…
分析:(1)由已知f(2)=1可求a
(2)由(1)得

,利用单调性的定义,设任意x
1,x
2∈(-∞,0),且x
1<x
2.判断

的符号即可证明
点评:本题主要考查了利用待定系数法求解函数解析式,函数单调性的定义在证明单调性中的应用,属于基础试题
练习册系列答案
相关习题
科目:高中数学
来源:
题型:
已知函数y=f(2-3x)在区间(1,2)单调递减,那么函数y=f(x)( )
|
|
|
|
查看答案和解析>>
科目:高中数学
来源:2011-2012学年广东省广州六中高三(上)第三次月考数学试卷(文科)(解析版)
题型:选择题
已知函数
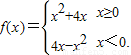
若f(2-a
2)>f(a),则实数a的取值范围是( )
A.(-∞,-1)∪(2,+∞)
B.(-1,2)
C.(-2,1)
D.(-∞,-2)∪(1,+∞)
查看答案和解析>>
科目:高中数学
来源:2013年上海市长宁区高考数学一模试卷(文科)(解析版)
题型:选择题
已知函数
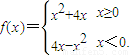
若f(2-a
2)>f(a),则实数a的取值范围是( )
A.(-∞,-1)∪(2,+∞)
B.(-1,2)
C.(-2,1)
D.(-∞,-2)∪(1,+∞)
查看答案和解析>>
科目:高中数学
来源:2011年高三数学(理科)一轮复习讲义:2.2 函数的单调性与最大(小)值(解析版)
题型:选择题
已知函数
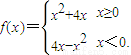
若f(2-a
2)>f(a),则实数a的取值范围是( )
A.(-∞,-1)∪(2,+∞)
B.(-1,2)
C.(-2,1)
D.(-∞,-2)∪(1,+∞)
查看答案和解析>>
科目:高中数学
来源:广东省高考数学一轮复习:3.7 函数的单调性(解析版)
题型:选择题
已知函数
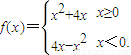
若f(2-a
2)>f(a),则实数a的取值范围是( )
A.(-∞,-1)∪(2,+∞)
B.(-1,2)
C.(-2,1)
D.(-∞,-2)∪(1,+∞)
查看答案和解析>>

 ,f(2)=1.
,f(2)=1.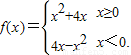 若f(2-a2)>f(a),则实数a的取值范围是( )
若f(2-a2)>f(a),则实数a的取值范围是( )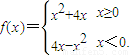 若f(2-a2)>f(a),则实数a的取值范围是( )
若f(2-a2)>f(a),则实数a的取值范围是( )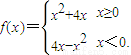 若f(2-a2)>f(a),则实数a的取值范围是( )
若f(2-a2)>f(a),则实数a的取值范围是( )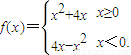 若f(2-a2)>f(a),则实数a的取值范围是( )
若f(2-a2)>f(a),则实数a的取值范围是( )