
今有甲、乙两个篮球队进行比赛,规定两队中有一队胜4场,则整个比赛宣告结束,假设甲、乙两队在每场比赛中获胜的概率都是![]() ,并记需要比赛的场数为ξ.求:
,并记需要比赛的场数为ξ.求:
(1)ξ
大于5的概率;(2)ξ
的分布列和数学期望.科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源:广东省佛山一中2010-2011学年高二下学期期末考试数学(理) 题型:解答题
(14分)今有甲、乙两个篮球队进行比赛,比赛采用7局4胜制.假设甲、乙两队在每场比赛中获胜的概率都是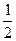 .并记需要比赛的场数为ξ.
.并记需要比赛的场数为ξ.
(Ⅰ)求ξ大于5的概率;(Ⅱ)求ξ的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源:广东省2012届高二下学期期末考试数学(理) 题型:解答题
(14分)今有甲、乙两个篮球队进行比赛,比赛采用7局4胜制.假设甲、乙两队在每场比赛中获胜的概率都是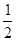 .并记需要比赛的场数为ξ.
.并记需要比赛的场数为ξ.
(Ⅰ)求ξ大于5的概率;(Ⅱ)求ξ的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省荆州市江陵实验高中高二(上)综合测试数学试卷(解析版) 题型:解答题
 .并记需要比赛的场数为X.
.并记需要比赛的场数为X.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com