
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
![]()
这是一道较平常的排列组合问题,解法较多,一般从类似于下面思路去考虑:
分析:第1格与第8格必选,故只有2、3、4、5、6、7格可省(省格不超过3,也不能连省2格).
每格必过的方案1种;
省1格的方案6种;
省2格的方案4+3+2+1=10种;
省3格的方案3+1=4种;
总共有1+6+10+4=21种.此法很难用于多格.
下面再介绍两种解法:
法一:(插空法)从2、3、4、5、6、7格中,将“要省格”去插“不省格”留下的空,则有:
每格必过(省0格)的方案
·|·|·|·|·|·|·(7个空)![]() 种;
种;
省1格的方案
·|·|·|·|·|· (6个空)![]() 种;
种;
省2格的方案
·|·|·|·|· (5个空)![]() 种;
种;
省3格的方案
·|·|·|· (4个空)![]() 种;
种;
总共有![]() +
+![]() +
+![]() +
+![]() =21种.用此法很容易将此题推广到n格,得到跳动法种数为
=21种.用此法很容易将此题推广到n格,得到跳动法种数为![]() +… (n为奇数时,末项是
+… (n为奇数时,末项是![]() ,n为偶数时,末项是
,n为偶数时,末项是![]() ).
).
法二:当n≥3时,人到第n格只能是:①从第n-2格跳进,②从第n-1格跳(走)进两种方式,那么人到第n格方法数为第n-2格方法数与第n-1格方法数之和:
人到第1格 1种;
人到第2格 1种;
人到第3格 1+1=2种;
人到第4格 1+2=3种;
人到第5格 2+3=5种;
人到第6格 3+5=8种;
人到第7格 5+8=13种;
人到第8格 8+13=21种;
由此可得到结论:人到第n格的方法数为斐波那契数列:1,1,2,3,5,8,13,21,34,……的第n项an.
数列{an}中,a1=1,a2=1,且an+2=an+1+an,
由特征方程r2=r+1,得r=![]() ,
,
an=(![]() )nc1+(
)nc1+(![]() )nc2.
)nc2.
由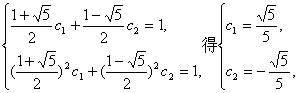
∴an=![]() [(1+
[(1+![]() )n-(1-
)n-(1-![]() )n](n∈N).
)n](n∈N).
上述两法不仅有“思维体操”美,也意外地得到了一个组合数恒等式:![]() +……=
+……=![]() [(1+
[(1+![]() )n-(1-
)n-(1-![]() )n](n∈N).
)n](n∈N).


科目:高中数学 来源: 题型:单选题

查看答案和解析>>
科目:高中数学 来源:2010年江西师大附中高考数学三模试卷(理科)(解析版) 题型:选择题

查看答案和解析>>
科目:高中数学 来源:《计数原理》2013年高三数学一轮复习单元训练(上海交大附中)(解析版) 题型:选择题

查看答案和解析>>
科目:高中数学 来源:2010年广西南宁市高考数学二模试卷(文科)(解析版) 题型:选择题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com