练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图1-6-4，某人身高a=1.77米，在黄浦江边测得对岸的东方明珠塔尖的仰角α=75.5°，测得在黄浦江中塔尖倒影的俯角β=75.6°，求东方明珠的塔高h.

    图1-6-4
    答案：
    解析：

    		 解：设黄浦江的宽为b米，则b·tanα=h-a,b·tanβ=h+a.

    消去b得h=·a=·a.

    当α=75.5°，β=75.6°，a=1.77米时，h=490.1米.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    某人设计一项单人游戏，规则如下：先将一棋子放在如图所示正方形ABCD（边长为3个单位）的顶点A处，然后通过掷骰子来确定棋子沿正方形的边按逆时针方向行走的单位，如果掷出的点数为i（i=1，2，3，4，5，6），则棋子就按逆时针方向行走i个单位，一直循环下去…．则某人抛掷三次骰子后，棋子恰好又回到点A处的所有不同走法共有
    25
    25
    种．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

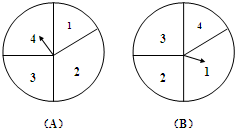    （2010•珠海二模）如图是两个独立的转盘（A）、（B），在两个图中的四个扇形区域的圆心角分别为60°、120°、90°90°．用这两个转盘进行玩游戏，规则是：同时转动两个转盘待指针停下（当两个转盘中任意一个指针恰好落在分界线时，则这次转动无效，重新开始），记转盘（A）指针所对的区域数为x，转盘（B）指针所对的区域数为y，x、y∈{1，2，3，4}，设x+y的值为ξ，每一次游戏得到奖励分为ξ．
    （1）求x＜3且y＞2的概率；
    （2）某人进行了6次游戏，求他平均可以得到的奖励分．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图所示,在墙上挂着一块边长为16 cm的正方形木板,上面画了小、中、大三个同心圆,半径分别为2 cm、4 cm、6 cm,某人站在3 m之外向此板投镖.设投镖击中线上或没有投中木板时都不算,可重投,问:

    (1)投中大圆内的概率是多少？

    (2)投中小圆与中圆形成的圆环的概率是多少？

    (3)投中大圆之外的概率是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图1-6-4，某人身高a=1.77米，在黄浦江边测得对岸的东方明珠塔尖的仰角α=75.5°，测得在黄浦江中塔尖倒影的俯角β=75.6°，求东方明珠的塔高h.

    图1-6-4

    查看答案和解析>>

    同步练习册答案