
甲、乙、丙三人独立破译同一份密码,已知甲、乙、丙各自破译出密码的概率分别为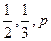 .且他们是否破译出密码互不影响.若三人中只有甲破译出密码的概率为
.且他们是否破译出密码互不影响.若三人中只有甲破译出密码的概率为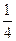 .
.
(Ⅰ)求甲乙二人中至少有一人破译出密码的概率;
(Ⅱ)求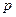 的值;
的值;
(Ⅲ)设甲、乙、丙三人中破译出密码的人数为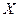 ,求
,求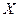 的分布列和数学期望
的分布列和数学期望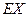 .
.
解:记“甲、乙、丙三人各自破译出密码”分别为事件
科目:高中数学
来源:
题型:
科目:高中数学
来源:
题型:
科目:高中数学
来源:
题型:
科目:高中数学
来源:2014届内蒙古赤峰市高三摸底考试理科数学试卷(解析版)
题型:解答题
甲、乙、丙三人独立破译同一份密码,已知甲、乙、丙各自破译出密码的概率分别为 且他们是否破译出密码互不影响,若三人中只有甲破译出密码的概率为 (1)求 (2)设在甲、乙、丙三人中破译出密码的总人数为X,求X的分布列和数学期望E(X).
科目:高中数学
来源:2013届陕西省西安市高二下学期期中理科数学试卷(解析版)
题型:解答题
甲、乙、丙三人独立破译同一份密码,已知甲、乙、丙各自破译出密码的概率分别为 (Ⅰ)求甲乙二人中至少有一人破译出密码的概率; (Ⅱ)求 (Ⅲ)设甲、乙、丙三人中破译出密码的人数为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区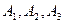 ,依题意有
,依题意有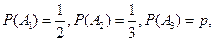 且
且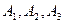 相互独立.
相互独立.
(Ⅰ)甲、乙二人中至少有一人破译出密码的概率为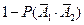
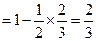 . …………………3分
. …………………3分
(Ⅱ)设“三人中只有甲破译出密码”为事件 ,则有
,则有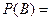
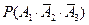 =
=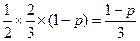 , …………………5分
, …………………5分
所以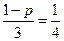 ,
,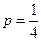 . ……………………7分
. ……………………7分
(Ⅲ)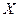 的所有可能取值为
的所有可能取值为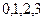 . ……………………8分
. ……………………8分
所以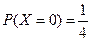 ,
,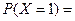
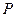
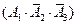
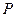
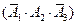
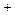
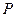
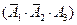
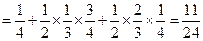 ,
,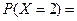
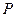
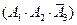
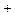
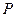
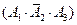
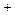
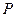
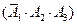
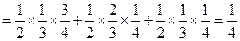 ,
,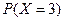 =
=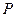
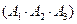 =
=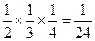 . ……………………11分
. ……………………11分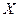 分布列为:
分布列为: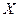
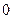
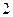

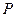
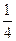
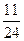
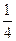
解析


小考实战系列答案
小考复习精要系列答案
小考总动员系列答案
小升初必备冲刺48天系列答案
68所名校图书小升初高分夺冠真卷系列答案
伴你成长周周练月月测系列答案
小升初金卷导练系列答案
萌齐小升初强化模拟训练系列答案
小升初全能卷系列答案
小升初全优模拟大考卷系列答案
,1 2
,p.且他们是否破译出密码互不影响.若三人中只有甲破译出密码的概率为1 3
.1 4
(Ⅰ)求甲乙二人中至少有一人破译出密码的概率;
(Ⅱ)求p的值;
(Ⅲ)设甲、乙、丙三人中破译出密码的人数为X,求X的分布列和数学期望EX.
,1 3
,p,且他们是否破译出密码互不影响,若三人中只有甲破译出密码的概率为1 4
.1 6
(1)求p的值,
(2)设在甲、乙、丙三人中破译出密码的总人数为X,求X的分布列和数学期望E(X).
、1 2
、p,且他们是否破译出密码互不影响,若三人中只有甲破译出密码的概率为1 3
.1 4
(1)求p的值.
(2)设甲、乙、丙三人中破译出密码的人数为X,求X的分布列和数学期望E(X).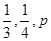 ,
,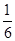 .
.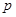 的值,
的值,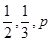 .且他们是否破译出密码互不影响.若三人中只有甲破译出密码的概率为
.且他们是否破译出密码互不影响.若三人中只有甲破译出密码的概率为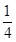 .
.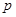 的值;
的值;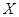 ,求
,求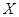 的分布列和数学期望
的分布列和数学期望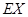 .
.
版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。
ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号