
过一点作圆的切线,求切线方程.现利用点斜式,求出斜率值只有一个,那该点在圆上吗?再想一想利用点斜式求直线方程,会产生漏解吗?如果漏解,那会漏掉什么样的解呢?
|
利用点斜式求直线方程时,很重要的一点就是注意点斜式不能表示斜率不存在的直线的方程,即倾斜角为 |
|
根据不同条件求圆的切线,主要有以下题型: (1)已知切点,求切线方程.可根据切线垂直于过切点的半径直接写出切线的方程.注意只有一条. (2)已知圆外一点,求圆的切线方程.切记有两条. (3)已知切线的斜率求圆的切线方程. 求圆的切线方程常用的三种方法: (1)设切点用切线公式法; (2)设切线斜率用判别式法; (3)设切线斜率,用圆心到切线的距离等于半径法. |


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
 (2011•崇明县二模)如图,已知椭圆
(2011•崇明县二模)如图,已知椭圆| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 3 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
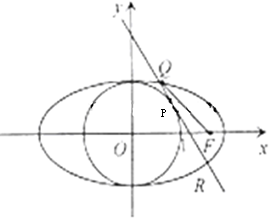 已知椭圆C:
已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:全优设计必修二数学苏教版 苏教版 题型:038
如果过一点作圆的切线,求切线方程.现利用点斜式,求出斜率值只有一个,那该点在圆上吗?再想一想利用点斜式求直线方程,会产生漏解吗?如果漏解,那会漏掉什么样的解呢?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com