已知f(x)=x3-ax2-3x
(1)若f(x)在[2,+∞)上是增函数,求实数a的取值范围;
(2)若x=3是f(x)的极值点,求f(x)在[1,a]上的最小值和最大值.
【答案】
分析:(1)因为f(x)在x∈[1,+∞)上是增函数,所以令f′(x)>0,解得
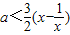
,求出
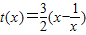
的最小值得到a的取值范围.
(2)由f'(3)=0,得a=4,从而有f(x)在(1,3)上为减函数,在(3,4)上为增函数,∴x=3时f(x)有极小值,从而确定最小值和最大值.
解答:解:(1)由题知,f'(x)=3x
2-2ax-3,令f'(x)>0(x≥2),得
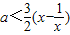
.
记
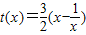
,当x≥2时,t(x)是增函数,∴
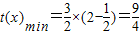
,∴
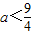
,又
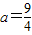
时,
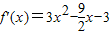
=3
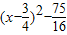
在[2,+∞)上恒大于等于0,∴
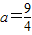
也符合题意,∴
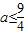
.
(2)由题意,得f'(3)=0,即27-6a-3=0,∴a=4,∴f(x)=x
3-4x
2-3x,f'(x)=3x
2-8x-3.
令f'(x)=0,得
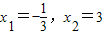
,
又∵x∈[1,4],∴
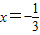
舍,故x=3,
当x∈(1,3),f'(x)<0,∴f(x)在(1,3)上为减函数;
当x∈(3,4),f'(x)>0,∴f(x)在(3,4)上为增函数,∴x=3时f(x)有极小值.
于是,当x∈[1,4]时,f(x)
min=f(3)=-18,
而f(1)=-6,f(4)=-12,∴f(x)
max=f(1)=-6.
点评:考查学生利用导数研究函数的单调性的能力,利用导数求闭区间上函数最值的能力.

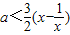 ,求出
,求出 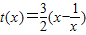 的最小值得到a的取值范围.
的最小值得到a的取值范围.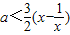 .
.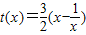 ,当x≥2时,t(x)是增函数,∴
,当x≥2时,t(x)是增函数,∴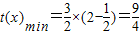 ,∴
,∴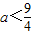 ,又
,又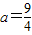 时,
时,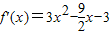 =3
=3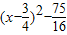 在[2,+∞)上恒大于等于0,∴
在[2,+∞)上恒大于等于0,∴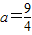 也符合题意,∴
也符合题意,∴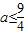 .
.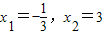 ,
,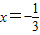 舍,故x=3,
舍,故x=3,
