【答案】
分析:(1)把已知两式平方相加,结合两角差的余弦公式可得;(2)两式平方相减可得cos2α+2cos(α+β)+cos2β=2,再利用整体角α+β,α-β表示式子中的角应用公式可得cos(α+β)cos(α-β)+cos(α+β)=1,把(1)的结果代入即可.
解答:解:(1)因为sinα+sinβ=1 ①cosα+cosβ=
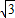
②
两式平方相加可得:得sin
2α+2sinαsinβ+sin
2β+cos
2α+2sinαsinβ+cos
2β=4 (3分)
即2+2cos(α-β)=4,所以cos(α-β)=1;(6分)
(2)②
2-①
2得cos
2α-sin
2α+2cosαcosβ-2sinαsinβ+cos
2β-sin
2β=2
即cos2α+2cos(α+β)+cos2β=2 (8分)
故cos[(α+β)+(α-β)]+2cos(α+β)+cos[(α+β)-(α-β)]=2 (12分)
化简得cos(α+β)cos(α-β)+cos(α+β)=1,
由(1)得
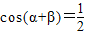
.(14分)
点评:本题为三角函数公式的综合应用,熟记公式并能利用整体角的思想是解决问题的关键,属中档题.

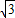 .
.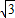 ②
②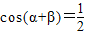 .(14分)
.(14分)

 高效智能课时作业系列答案
高效智能课时作业系列答案