Question

设A(-c,0)、B(c,0)(c＞0)为两定点,动点P到A点的距离与到B点的距离的比为定值a(a＞0),求P点的轨迹.

Answer 1

剖析：给曲线建立方程是解析几何的两个主要问题之一,其基本方法就是把几何条件代数化;主要问题之二是根据方程研究曲线的形状、性质,即用代数的方法研究几何问题.

解：设动点P的坐标为(x,y),由=a(a＞0)得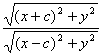=a,化简,

    得(1-a²)x²+2c(1+a²)x+c²(1-a²)+(1-a²)y²=0.

    当a=1时,方程化为x=0.

    当a≠1时,方程化为(x-c)²+y²=()².

    所以当a=1时,点P的轨迹为y轴;

    当a≠1时,点P的轨迹是以点(c,0)为圆心,||为半径的圆.

讲评：本题主要考查直线、圆、曲线和方程等基本知识,考查运用解析几何的方法解决问题的能力,对代数式的运算化简能力有较高要求.同时也考查了分类讨论这一数学思想.