练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图所示，B为△ACD所在平面处一点，M、N、G分别为△ABC、△ABD、△BCD的重心，(1)求证：平面MNG∥∶平面ACD；

    (2)求．

    答案：略
    解析：

    (1)证明：连结BM、BN、BG并延长交AC、AD、CD分别于P、F、H

    ∵M、N、G分别为△ABC、△ABD、△BCD的重心，

    则有．

    连结PF、FH、PH，有MN∥PF，

    又PF平面ACD，MN平面ACD，

    ∴MN∥平面ACD．

    同理MG∥平面ACD，MG∩MN=M，

    ∴平面MNG∥平面ACD．

    (2)解：由(1)可知：，∴．

    又PH=AD，∴MG=AD．

    同理NG=AC，MN=CD，

    ∴△MNG∽△ACD，其相似比为1∶3．

    ∴．

    　　要证明平面MNG∥平面ACD，由于M、N、G分别为△ABC、△ABD、△BCD的重心，因此可想到利用重心的性质找出与平面平行的直线．

    　　因为△MNG所在的平面与△ACD所在的平面相互平行，因此，求两三角形的面积之比，实则求这两个三角形的对应边之比．

    　　题目应用到面面平行的判定和相似三角形的性质．要注意综合运用所学知识解决问题．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    精英家教网三棱锥被平行于底面ABC的平面所截得的几何体如图所示，截面为A1B1C1，∠BAC=90°，A1A⊥平面ABC，A1A=
    		3
    ，AB=
    		2
    ，AC=2，A1C1=1，
    BD
    DC
    =
    1
    2
    ．
    （Ⅰ）证明：平面A1AD⊥平面BCC1B1；
    （Ⅱ）求二面角A-CC1-B的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

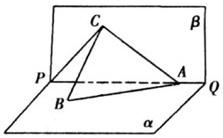    精英家教网如图所示，PQ为平面α、β的交线，已知二面角α-PQ-β为直二面角，A∈PQ，B∈α，C∈β，CA=CB=kAB（k∈R*），∠BAP=45°．
    （1）证明：BC⊥PQ；
    （2）设点C在平面α内的射影为点O，当k取何值时，O在平面ABC内的射影G恰好为△ABC的重心？
    （3）当k=
    		6
    3
    时，求二面角B-AC-P的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图所示，B点坐标为（-c，0），C点坐标为（c，0），AH⊥BC，垂足为H，且
    .
    BH
    =3
    .
    HC
    ．
    （1）若
    AB
    ?
    AC
    =0    ，求以B、C为焦点并且经过点A的椭圆的离心率；
    （2）
    AD
    =λ
    DB
    ，A、D同在以B、C为焦点的椭圆上，当-5≤λ≤
    7
    2
    时，求椭圆的离心率e的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    三次函数f（x）=x3+ax2+bx+c的图象如图所示，直线BD∥AC，且直线BD与函数图象切于点B，交于点D，直线AC与函数图象切于点C，交于点A．
    （1）若函数f（x）为奇函数且过点（1，-3），当x＜0时求
    f(x)+8xx2
    的最大值；
    （2）若函数在x=1处取得极值-2，试用c表示a和b，并求f（x）的单调递减区间；
    （3）设点A、B、C、D的横坐标分别为xA，xB，xC，xD求证    （xA-xB）：（xB-xC）：（xC-xD）=1：2：1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图所示，半径为r的四分之一的圆ABC上，分别以AB和AC为直径作两个半圆，分别标有α的阴影部分面积和标有b的阴影部分面积，则这两部分面积α和b有（　　）

    查看答案和解析>>

    同步练习册答案