
已知实数a,b满足 ,则函数f(x)=
,则函数f(x)=  的两个极值点都在(0,1)内的概率为______
的两个极值点都在(0,1)内的概率为______

【解析】
试题分析:本题考查的知识点是几何概型的意义,关键是要找出函数f(x)=  有极值对应的可行域面积的大小和实数a,b满足
有极值对应的可行域面积的大小和实数a,b满足 对应的图形面积的大小。
对应的图形面积的大小。
∵函数f(x)=  ∴f′(x)=x2-2ax+b,
∴f′(x)=x2-2ax+b,
∵函数f(x)=  的两个极值点都在(0,1)内,
的两个极值点都在(0,1)内,
x2-2ax+b=0的两个根都在(0,1)内,
∴两根之和2a∈(0,2),两根之积b∈(0,1),
∴△=4a2-4b>0,0<a<1,0<b<1∵实数a,b满足 ,
,
∴如图所示,区域-1 a
a 1,-1
1,-1 b
b 1的面积(图中正方形所示)为4,
1的面积(图中正方形所示)为4,
a2>b在条件0<a<1,0<b<1下的面积(图中阴影所示)为 ,所求的概率为
,所求的概率为
考点:几何概型
点评:几何概型的概率估算公式中的“几何度量”,可以为线段长度、含面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.解决的步骤均为:求出满足条件A的基本事件对应的“几何度量”N(A),再求出总的基本事件对应的“几何度量”N,最后根据公式求解.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
A.|a+b|>|a-b| B.|a+b|<|a-b|
C.|a-b|<||a|-|b|| D.|a-b|<|a|+|b|
查看答案和解析>>
科目:高中数学 来源: 题型:
①0<b<a ②a<b<0 ③0<a<b ④b<a<0 ⑤a=b
其中不可能成立的关系式有( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:高中数学 来源:2012-2013学年河南省郑州市高三第十四次调考理科数学试卷(解析版) 题型:填空题
已知实数a,b满足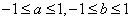 ,则函数f(x)=
,则函数f(x)= 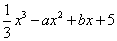 的两个极值点都在(0,1)内的概率为______
的两个极值点都在(0,1)内的概率为______
查看答案和解析>>
科目:高中数学 来源:2010-2011学年西藏拉萨中学高三第六模拟考试数学理卷 题型:选择题
已知实数a,b满足a+2b=1,则2a+4b的最小值是
A.2
B.2 C.4
D.4
C.4
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com