已知等比数列{an}及等差数列{bn},其中b1=0,公差d≠0.将这两个数列的对应项相加,得一新数列1,1,2,…,则这个新数列的前10项之和为________.
978
分析:设等比数列{a
n}的公比为q,则由题意可得 a
1+0=1,a
1q+d=1,
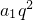
+2d=2,求出a
1、q、d的值,
可得a
n=2
n-1,b
n =1-n.再把等比数列的前10项和加上等差数列的前10项和,即为所求.
解答:设等比数列{a
n}的公比为q,则由题意可得 a
1+0=1,a
1q+d=1,
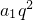
+2d=2.
解得 a
1=1,q=2,d=-1.
故有a
n=2
n-1,b
n =0+(n-1)(-1)=1-n.
故新数列的通项为c
n=a
n+b
n =2
n-1+1-n.
故这个新数列的前10项之和等于等比数列的前10项和加上等差数列的前10项和,
即

+

=978,
故答案为978.
点评:本题主要考查等差数列的通项公式,前n项和公式及其应用,用拆项法进行数列求和,属于中档题.

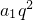 +2d=2,求出a1、q、d的值,
+2d=2,求出a1、q、d的值,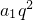 +2d=2.
+2d=2. +
+ =978,
=978,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案