
设函数
(1)若关于x的不等式 在
在 有实数解,求实数m的取值范围;
有实数解,求实数m的取值范围;
(2)设 ,若关于x的方程
,若关于x的方程 至少有一个解,求p的最小值.
至少有一个解,求p的最小值.
(3)证明不等式:

(1) (2)p的最小值为0
(2)p的最小值为0
【解析】
试题分析:
(1)存在性问题,只需要 即可,再利用导数法求解f(x)的最大值(即求导,求单调性,求极值9与端点值比较得出最值).
即可,再利用导数法求解f(x)的最大值(即求导,求单调性,求极值9与端点值比较得出最值).
(2)p的最小值为函数g(x)的最小值,利用导数求函数的最小值即可(即求导,求单调性,求极值9与端点值比较得出最值).
(3)利用第二问结果可以得到与不等式有关的恒等式 .令
.令 .把n=1,2,3,,得n个不等式左右相加,左边利用对数除法公式展开即可用裂项求和法得到不等式的左边,即证得原式
.把n=1,2,3,,得n个不等式左右相加,左边利用对数除法公式展开即可用裂项求和法得到不等式的左边,即证得原式
试题解析:
(1)依题意得
 ,而函数
,而函数 的定义域为
的定义域为
∴ 在
在 上为减函数,在
上为减函数,在 上为增函数,则
上为增函数,则 在
在 上为增函数
上为增函数
, 即实数m的取值范围为
即实数m的取值范围为 4分
4分
(2)
 则
则
显然,函数 在
在 上为减函数,在
上为减函数,在 上为增函数,则函数
上为增函数,则函数 的最小值为
的最小值为
所以,要使方程 至少有一个解,则
至少有一个解,则 ,即p的最小值为0 8分
,即p的最小值为0 8分
(3)由(2)可知:  在
在 上恒成立
上恒成立
所以  ,当且仅当x=0时等号成立
,当且仅当x=0时等号成立
令 ,则
,则 代入上面不等式得:
代入上面不等式得:
即 , 即
, 即 
所以, ,
, ,
, ,,
,,
将以上n个等式相加即可得到: 12分
12分
考点:导数 不等式 函数最值


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源:2012-2013学年陕西省高三第二次教学质量检测理科数学试卷(解析版) 题型:解答题
设函数
(1)若关于x的不等式 在
在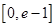 有实数解,求实数m的取值范围;
有实数解,求实数m的取值范围;
(2)设 ,若关于x的方程
,若关于x的方程 至少有一个解,求
至少有一个解,求 的最小值.
的最小值.
(3)证明不等式:
查看答案和解析>>
科目:高中数学 来源:2011-2012学年陕西省高三第七次适应性训练理科数学(解析版) 题型:解答题
设函数
(1)若关于x的不等式 在
在 有实数解,求实数m的取值范围;
有实数解,求实数m的取值范围;
(2)设 ,若关于x的方程
,若关于x的方程 至少有一个解,求p 的最小值.
至少有一个解,求p 的最小值.
(3)证明不等式:

查看答案和解析>>
科目:高中数学 来源:2011-2012学年河北省高三上学期2月月考理科数学试卷 题型:解答题
设函数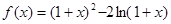
(1)若关于x的不等式 在
在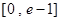 有实数解,求实数m的取值范围;
有实数解,求实数m的取值范围;
(2)设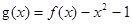 ,若关于x的方程
,若关于x的方程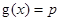 至少有一个解,求p 的最小值.
至少有一个解,求p 的最小值.
(3)证明不等式:
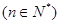
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河北省五校联盟模拟考试理科数学试卷 题型:解答题
设函数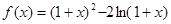
(1)若关于x的不等式 在
在 有实数解,求实数m的取值范围;
有实数解,求实数m的取值范围;
(2)设 ,若关于x的方程
,若关于x的方程 至少有一个解,求p 的最小值.
至少有一个解,求p 的最小值.
(3)证明不等式:

查看答案和解析>>
科目:高中数学 来源:2011-2012学年四川省高三一诊模拟考试理科数学试卷 题型:解答题
设函数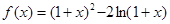
(1)若关于x的不等式 在
在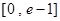 有实数解,求实数m的取值范围;
有实数解,求实数m的取值范围;
(2)设 ,若关于x的方程
,若关于x的方程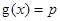 至少有一个解,求p 的最小值.
至少有一个解,求p 的最小值.
(3)证明不等式:
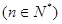
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com