
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
下列命题中不正确的是
A.若A+B+C=0,则直线Ax+By+C=0必过定点
B.直线Ax+By+C=0与Bx-Ay+C=0恒有交点
C.设A·B≠0,过定点(x0,y0)且与直线Ax+By+C=0垂直的直线的方程是![]() =
=![]()
D.过点(2,3)且在两坐标轴上的截距的绝对值相等的直线有且只有两条
查看答案和解析>>
科目:高中数学 来源: 题型:
定义在R上的奇函数f(x)为减函数,设a+b≤0,给出下列不等式:①f(a)·f(-a)≤0;②f(b)·f(-b)≥0;③f(a)+f(b)≤f(-a)+f(-b);④f(a)+f(b)≥f(-a)+f(-b)。其中正确的不等式序号是( )
A.①②④ B.①④ C.②④ D.①③
查看答案和解析>>
科目:高中数学 来源:2010-2011学年安徽省、岳西中学高三上学期联考理科数学卷 题型:填空题
定义在R上的奇函数,f(x)是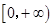 上的减函数,设a+b≤0,给出下列不等式:
上的减函数,设a+b≤0,给出下列不等式:
① f(a+b)≥0; ② f(a+b)≤0;
③ f(a)+f(b)≤f(-a)+f(-b); ④ f(a)+f(b)≥f(-a)+f(-b)。
其中正确的不等式序号是___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com