练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知曲线。求曲线C与线段AB有两个不同交点的充要条件。

            

                                                  

    解：线段AB的方程为

                       将它代入方程                   得

                      

                       设上有两个不同的根的充要条件是

                      

                       为所求．


    解析:

    此题求的是两曲线有两个不同的充要条件，也就是说所求出的“条件”应满足：两曲线有两个不同交点，则应有“条件”成立；反之，“条件”成立，则两曲线有两个不同交点。具体分析此题所给曲线C是一条开口向下的抛物线，线段AB是直线上的一段，其中，按求曲线交点的方法，应将代入方程，

    得。使此方程在上有两个不同的根，即可。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知曲线C上的动点M（x，y）满足到点（1，0）的距离比到直线x=-2的距离小1．
    （1）求曲线C的方程；
    （2）过点P（2，4）的直线与曲线C交于A、B两点，在线段AB上取点Q，满足|
    AP
    |•|
    QB
    |=|
    AQ
    |•|
    PB
    |，证明：
    （ⅰ）
    1
    |
    PA
    |
    +
    1
    |
    PB
    |
    =
    2
    |
    PQ
    |
    ；（ⅱ）点Q总在某定直线上．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学江苏省无锡市青阳高级中学高三（上）月考数学试卷（一）（解析版） 题型：解答题

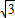    已知曲线C上动点P（x，y）到定点F1（，0）与定直线l1：x=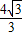的距离之比为常数．
    （1）求曲线C的轨迹方程；
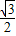    （2）以曲线c的左顶点T为圆心作圆T：（x+2）2+y2=r2（r＞0），设圆T与曲线C交于点M与点N，求•的最小值，并求此时圆T的方程．

    查看答案和解析>>

    科目：高中数学 来源：2008-2009学年浙江省杭州二中高三（上）1月月考数学试卷（理科）（解析版） 题型：解答题

    已知曲线C上的动点M（x，y）满足到点（1，0）的距离比到直线x=-2的距离小1．
    （1）求曲线C的方程；
    （2）过点P（2，4）的直线与曲线C交于A、B两点，在线段AB上取点Q，满足|•||•||，证明：
    （ⅰ）；（ⅱ）点Q总在某定直线上．

    查看答案和解析>>

    科目：高中数学 来源：2012年上海市崇明县高考数学二模试卷（理科）（解析版） 题型：解答题

    已知曲线C上动点P（x，y）到定点F1（，0）与定直线l1：x=的距离之比为常数．
    （1）求曲线C的轨迹方程；
    （2）若过点Q（1，）引曲线C的弦AB恰好被点Q平分，求弦AB所在的直线方程；
    （3）以曲线C的左顶点T为圆心作圆T：（x+2）2+y2=r2（r＞0），设圆T与曲线C交于点M与点N，求的最小值，并求此时圆T的方程．

    查看答案和解析>>

    同步练习册答案