
(1)求MN的长.
(2)当a为何值时,MN的长最短?并求出|MN|的最小值.
活动:学生思考或讨论,师生共同探讨解题方法,此题的求解方法很多,但利用坐标法求解既简单,又易行,我们必须建立适当的空间直角坐标系,利用空间两点间的距离公式求MN的长,求|MN|的最小值,我们可构建关于a的函数,利用函数的最值来解决.
解:∵平面ABCD⊥平面ABEF,且平面ABCD∩平面ABEF=AB,AB⊥BE,∴BE⊥平面ABC.∴AB,BC,BE两两垂直.∴以B为原点,分别以射线BA,BE,BC为x轴、y轴、z轴的正方向,建立空间直角坐标系B—xyz,如图3.

图3
(1)∵正方形ABCD和正方形ABEF的边长都是1,CM=BN=a,
∴M(![]() a,0,1
a,0,1![]() a),N(
a),N(![]() a,
a, ![]() a,0).由空间两点间的距离公式得
a,0).由空间两点间的距离公式得
|MN|=![]() =
=![]() .
.
(2)由本题(1)可知|MN|=![]() ,其中0<a<
,其中0<a<![]() ,所以,当a=
,所以,当a=![]() 时,|MN|最短,|MN|的最小值为
时,|MN|最短,|MN|的最小值为![]() .此时,M,N恰为AC,BF的中点.
.此时,M,N恰为AC,BF的中点.
点评:运用空间点的坐标运算解决几何问题时,首先建立适当的空间直角坐标系,计算出相关点的坐标,进行求解.在建立空间直角坐标系时,应注意原点的选择,原点的选择要便于解决问题,既有利于作图的直观性,又要知尽可能的使点的坐标为正值.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:
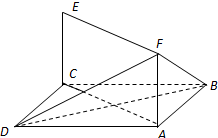 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=| 2 |
| PF |
| DA |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
如图所示,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,BC⊥AC,EF∥AC,AB=
在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,BC⊥AC,EF∥AC,AB=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
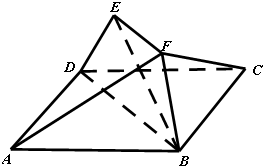 (2012•江苏二模)如图,已知正方形ABCD和直角梯形BDEF所在平面互相垂直,BF⊥BD,EF=BF=
(2012•江苏二模)如图,已知正方形ABCD和直角梯形BDEF所在平面互相垂直,BF⊥BD,EF=BF=| 1 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com