
证法一:(作差比较法)
2sin2α![]()
![]()
∵α∈(0,π),
∴sinα>0,1-cosα>0,(2cosα-1)2≥0.
∴2sin2α![]() ≤0.
≤0.
∴2sin2α≤![]() .
.
证法二:(作商比较法)
∵0<α<π,∴sinα>0,1-cosα>0.
∴![]() >0.
>0.
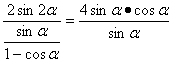 ·(1-cosα)
·(1-cosα)
=4cosα(1-cosα)
=1-(2cosα-1)2≤1,
∴2sin2α≤![]() .
.
证法三:(分析法)
要证明2sin2α≤![]() 成立,
成立,
只要证明4sinαcosα≤![]() .
.
∵α∈(0,π),∴sinα>0.
只要证明4cosα≤![]() .
.
上式可变形为4≤![]() +4(1-cosα).
+4(1-cosα).
∵1-cosα>0,
∴![]() +4(1-cosα)≥
+4(1-cosα)≥![]() =4,
=4,
当且仅当cosα=![]() ,即α=
,即α=![]() 时取等号.
时取等号.
∴4≤![]() +4(1-cosα)成立.
+4(1-cosα)成立.
∴不等式2sin2α≤![]() 成立.
成立.
证法四:(综合法)
∵![]() +4(1-cosα)≥4,
+4(1-cosα)≥4,
(1-cosα>0,当且仅当cosα=![]() 即α=
即α=![]() 时,取等号)
时,取等号)
∴4cosα≤![]() .
.
∵α∈(0,π),∴sinα>0.
∴4sinαcosα≤![]() .
.
∴2sin2α≤![]() .
.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com