
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省威海市高三第一次模拟考试理科数学试卷 题型:解答题
(本小题满分12分)现有正整数1,2,3,4,5,…n,一质点从第一个数1出发顺次跳动,质点的跳动步数通过抛掷骰子来决定:骰子的点数小于等于4时,质点向前跳一步;骰子的点数大于4时,质点向前跳两步.
(I)若抛掷骰子二次,质点到达的正整数记为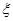 ,求E
,求E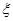 ;
;
(II)求质点恰好到达正整数5的概率.
查看答案和解析>>
科目:高中数学 来源:2012年山东省威海市高考数学一模试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:四川省南充高中08-09学年高二下学期第四次月考(理) 题型:解答题
(15分 注意:全部要算出数字来)现有0、1、2、3、4、5、6、7、8、9共十个数字.
⑴ 可以组成多少个无重复数字的三位数?
⑵ 组成无重复数字的三位数中,315是从小到大排列的第几个数?
⑶ 可以组成多少个无重复数字的四位偶数?
⑷ 选出一个偶数和三个奇数,组成无重复数字的四位数,这样的四位数有多少个?
⑸ 如果一个数各个数位上的数字从左到右按由大到小的顺序排列,则称此正整数为“渐减数”,那么由这十个数字组成的所有“渐减数”共有多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com