练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    平面α∥β,A、C∈α,B、D∈β,点E、F分别是线段AB、CD的中点，求证：EF∥β.

    分析一：可考虑由线线平行证明线面平行，即在β内找与EF平行的直线，而AB、CD的中点E、F使我们联想到中位线.?

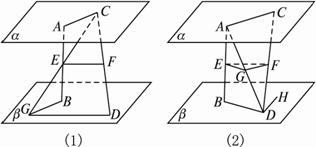
    证法一：如图(1)，设E与CD确定平面CEF，它与平面β交于GD,AB与CG确定的平面交α于AC，交β于GB，则由面面平行的性质定理可得AC∥GB.?

    ∵AE=BE,∴CE=GE.?

    又∵F是CD的中点，?

    ∴EF是△CGD的中位线，即EF∥GD，GDβ.?

    ∴EF∥β.

    分析二：证明线面平行，除了由线线平行外，还可利用面面平行证明，即过EF找或作一个平面，使之与β平行，E、F分别是AB、CD的中点仍然是解决问题的重要突破口.

    证法二：如图(2)，连结AD，取AD中点G，连结EG、FG.?

    ∵EG∥BD,BDβ,∴EG∥β.同理，GF∥α.?

    设平面ADC交β于DH.∵α∥β,∴AC∥DH.?

    ∴FG∥DH.∴GF∥β.?

    ∵EG∩GF=G,∴平面EGF∥β.?

    ∵EF平面EGF,∴EF∥β.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    精英家教网点P是△ABC所在平面外一点，A′，B′，C′分别是△PBC、△PCA、△PAB的重心．
    求证：（1）平面ABC∥平面A′B′C′；
    （2）求A′B′：AB．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    20、如图，A，B，C为不在同一条直线上的三点，AA′∥BB′∥CC′，且AA′=BB′=CC′，求证：平面ABC∥平面A′B′C′．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    11、线段AB长为5cm，在水平面上向右平移4cm后记为CD，将CD沿铅垂线方向向下移动3cm后记为C′D′，再将C′D′沿水平方向向左移4cm记为A′B′，依次连接构成长方体ABCD-A′B′C′D′．
    ①该长方体的高为
    3
    cm；
    ②平面A′B′C′D′与面CD D′C′间的距离为
    4
    cm；
    ③A到面BC C′B′的距离为
    5
    cm．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    P是△ABC所在平面外一点，A′、B′、C′分别是△PBC、△PCA、△PAB的重心，
    （1）求证：平面A′B′C′∥平面ABC；   
    （2）求S△A′B′C′：S△ABC．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    正方体ABCD-A/B/C/D/的棱长为8cm，M，N，P分别是AB，A/D/，BB/棱的中点．
    （1）画出过M，N，P三点的平面与平面A/B/C/D/及平面BB/C/C的交线，并说明画法的依据；
    （2）设过M，N，P三点的平面与B/C/交于点Q，求PQ的长．

    查看答案和解析>>

    同步练习册答案