练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设ξ为随机变量，从棱长为1的正方体的12条棱中任取两条，当两条棱相交时，ξ＝0；当两条棱平行时，ξ的值为两条棱之间的距离；当两条棱异面时ξ＝1．

    (1)求概率p(ξ＝0)

    (2)求ξ的分布列，并求其数学期望E(ξ)．

    答案：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （2012•江苏）设ξ为随机变量，从棱长为1的正方体的12条棱中任取两条，当两条棱相交时，ξ=0；当两条棱平行时，ξ的值为两条棱之间的距离；当两条棱异面时，ξ=1．
    （1）求概率P（ξ=0）；
    （2）求ξ的分布列，并求其数学期望E（ξ）．

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年江苏苏州市高三调研测试理科数学试卷（解析版） 题型：解答题

    设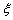为随机变量，从棱长为1的正方体ABCD?A1B1C1D1的八个顶点中任取四个点，当四点共面时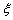，=0，当四点不共面时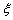，的值为四点组成的四面体的体积．

    （1）求概率P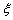（=0）；

    （2）求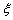的分布列，并求其数学期望E ()．

     

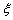    查看答案和解析>>

    科目：高中数学 来源：2012年全国普通高等学校招生统一考试数学（江苏卷解析版） 题型：解答题

    设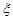为随机变量，从棱长为1的正方体的12条棱中任取两条，当两条棱相交时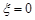，；当两条棱平行时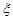，的值为两条棱之间的距离；当两条棱异面时，．

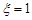      （1）求概率；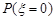

      （2）求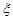的分布列，并求其数学期望．

     

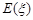    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年湖北省武汉六中高三（上）12月月考数学试卷（理科）（解析版） 题型：解答题

    设ξ为随机变量，从棱长为1的正方体的12条棱中任取两条，当两条棱相交时，ξ=0；当两条棱平行时，ξ的值为两条棱之间的距离；当两条棱异面时，ξ=1．
    （1）求概率P（ξ=0）；
    （2）求ξ的分布列，并求其数学期望E（ξ）．

    查看答案和解析>>

    科目：高中数学 来源：2012年江苏省高考数学试卷（解析版） 题型：解答题

    设ξ为随机变量，从棱长为1的正方体的12条棱中任取两条，当两条棱相交时，ξ=0；当两条棱平行时，ξ的值为两条棱之间的距离；当两条棱异面时，ξ=1．
    （1）求概率P（ξ=0）；
    （2）求ξ的分布列，并求其数学期望E（ξ）．

    查看答案和解析>>

    同步练习册答案