练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知向量m＝f(x)＝m·n．

    (Ⅰ)求函数f(x)的单调区间；

    (Ⅱ)如果先将f(x)的图象向左平移个单位，再保持纵坐标不变，横坐标变为原来的倍，得到函数g(x)的图象，若g(x)为偶函数，求的最小值．

    答案：
    解析：

    　　解：(Ⅰ)

    　　　　　　2分

    　　由

    　　∴的单调递增区间为

    　　由

    　　∴f(x)的单调递减区间为　　　　6分

    　　(Ⅱ)将f(x)的图象向左移个单位后得到的是函数

    　　的图象　　　　7分

    　　然后横坐标变为原来的倍，得到函数

    　　的图象　　　　9分

    　　∵g(x)为偶函数，

    　　∴∵，

    　　∴当k＝0时，有最小值　　　　　　12分


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2011届高考数学第一轮复习测试题6 题型：044

    (理)已知向量m＝(sinωx＋cosωx，cosωx)，n＝(cosωx－sinωx，2 sinωx)，其中ω＞0，函数f(x)＝m·n，若f(x)相邻两对称轴间的距离为．

    (1)求ω的值，并求f(x)的最大值及相应x的集合；

    (2)在△ABC中，a、b、c分别是A、B、C所对的边，△ABC的面积S＝5，b＝4，f(A)＝1，求边a的长．

    查看答案和解析>>

    科目：高中数学 来源：2014届江苏省高三10月质量检测文科数学试卷（解析版） 题型：解答题

    已知向量m＝(2sinx，cosx)，n＝(cosx,2cosx)，定义函数f(x)＝m·n－1．

    (1)求函数f(x)的最小正周期；

    (2)确定函数f(x)的单调区间、对称轴与对称中心．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届广东省高一暑假作业（六）必修4数学试卷（解析版） 题型：解答题

    已知向量m＝(sinA，cosA)，n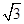＝(，－1)，m·n＝1，且A为锐角．

    (1)求角A的大小；

    (2)求函数f(x)＝cos2x＋4cosAsinx(x∈R)的值域．

     

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年湖南省长沙市高三第六次月考理科数学卷 题型：解答题

    (本小题满分12分)

    已知向量m＝(sin，1)，n＝(cos，cos2)，f(x)＝m·n.

    (1)若f(x)＝1，求cos(－x)的值；

    (2)在△ABC中，角A，B，C的对边分别是a，b，c且满足acosC＋c＝b，求函数f(B)的取值范围.

     

    查看答案和解析>>

    同步练习册答案