Question

已知偶函数f(x)=cosθsinx-sin(x-θ)+(tanθ-2)sinx-sinθ的最小值是0,求f(x)的最大值及此时x的集合.

Answer 1

解析：f(x)=cosθsinx-(sinxcosθ-cosxsinθ)+(tanθ-2)sinx-sinθ=sinθcosx+(tanθ-2)sinx-sinθ.

∵f(x)是偶函数,所以对任意x∈R,都有f(-x)=f(x)，

即sinθcos(-x)+(tanθ-2)sin(-x)-sinθ=sinθcosx+(tanθ-2)sinx-sinθ,

即(tanθ-2)sinx=0,

所以tanθ=2.

由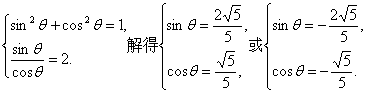

此时f(x)=sinθ(cosx-1).

当sinθ=时,f(x)=(cosx-1)，

最大值为0,不合题意舍去;

当sinθ=-时,f(x)=-(cosx-1)，最小值为0,当cosx=-1时,f(x)有最大值为,

自变量x的集合为{x|x=2kπ+π,k∈Z}.