练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如果函数f(x)在[a，b]上是增函数，对于任意的x1、x2∈[a，b](x1≠x2)，则下列结论中不正确的是

    (　　)

    A.>0

    B．(x1－x2)[f(x1)－f(x2)]＞0

    C．f(a)＜f(x1)＜f(x2)＜f(b)

    D.>0

    C　由函数单调性的定义可知，若函数y＝f(x)在给定的区间上是增函数，则x1－x2与f(x1)－f(x2)同号，由此可知，选项A、B、D正确；

    对于C，若x1<x2时，可有x1＝a或x2＝b，即f(x1)＝f(a)或f(x2)＝f(b)，故C不成立．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知关于x的函数f(x)=-
    1
    3
    x
    3
     
    +b
    x
    2
     
    +cx+bc    ，其导函数f′（x）．
    （1）如果函数f(x)在x=1处有极值-
    4
    3
    ，试确定b、c的值；
    （2）设当x∈（0，1）时，函数y=f（x）-c（x+b）的图象上任一点P处的切线斜率为k，若k≤1，求实数b的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （本小题满分14分）已知关于x的函数f(x)＝＋bx2＋cx＋bc，其导函数为f+(x)。令g(x)＝∣f+(x) ∣，记函数g(x)在区间[-1、1]上的最大值为M。

    （Ⅰ）如果函数f(x)在x＝1处有极值-，试确定b、c的值；

    （Ⅱ）若∣b∣>1，证明对任意的c，都有M>2；

    （Ⅲ）若M≥K对任意的b、c恒成立，试求k的最大值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知关于x的函数f(x)＝＋bx2＋cx＋bc,其导函数为f+(x).令g(x)＝∣f (x) ∣,记函数g(x)在区间[-1、1]上的最大值为M.

       (Ⅰ)如果函数f(x)在x＝1处有极值-，试确定b、c的值：

      （Ⅱ）若∣b∣>1,证明对任意的c,都有M>2: w.w.w.k.s.5.u.c.o.m    

       (Ⅲ)若M≧K对任意的b、c恒成立，试求k的最大值。

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年福建省高三上学期期中考试理科数学 题型：解答题

    （15分）设函数＝，∈R，为自然对数的底数，

    (1)如果＝为函数的极大值点，求的值；

    (2)如果函数f (x)在＝处的切线与坐标轴围成的三角形的面积等于，求的值；

    (3)在(2)的条件下，当时，求f (x)的最大值和最小值.

     

    查看答案和解析>>

    科目：高中数学 来源：新课标高三数学导数专项训练（河北） 题型：选择题

    已知函数f(x)是定义在R上的函数，如果函数f(x)在R上的导函数f′(x)的图象如图，则有以下几个命题：

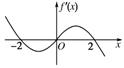
    (1)f(x)的单调递减区间是(－2,0)、(2，＋∞)，f(x)的单调递增区间是(－∞，－2)、(0,2)；

    (2)f(x)只在x＝－2处取得极大值；

    (3)f(x)在x＝－2与x＝2处取得极大值；

    (4)f(x)在x＝0处取得极小值．

    其中正确命题的个数为                                                               (　　)

    A．1                                               B．2

    C．3                                               D．4

     

    查看答案和解析>>

    同步练习册答案