
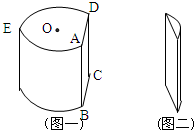
 如图,点O为圆柱形木块底面的圆心,AD是底面圆的一条弦,优弧$\widehat{AED}$的长为底面圆的周长的$\frac{3}{4}$.过AD和母线AB的平面将木块剖开,得到截面ABCD,已知四边形ABCD的周长为40.
如图,点O为圆柱形木块底面的圆心,AD是底面圆的一条弦,优弧$\widehat{AED}$的长为底面圆的周长的$\frac{3}{4}$.过AD和母线AB的平面将木块剖开,得到截面ABCD,已知四边形ABCD的周长为40.分析 (I)利用△AOD为等腰直角三角形,⊙O的半径r=$\frac{\sqrt{2}}{2}$|AD|.
(Ⅱ)依题意得,四边形ABCD为矩形,可得所求几何体的侧面积S=x(20-x)+$\frac{3}{4}×2π×\frac{\sqrt{2}}{2}$x(20-x),再利用二次函数的单调性即可得出.
解答 解:(Ⅰ)∵优弧AED的长为底面周长为$\frac{3}{4}$,
∴∠AOD=90°,
∴△AOD为等腰直角三角形,
∴⊙O的半径$r=\frac{{\sqrt{2}}}{2}|AD|=\frac{{\sqrt{2}}}{2}x$.
(Ⅱ)依题意得,四边形ABCD为矩形,
∵四边形ABCD的周长为40,
∴AB=20-AD=20-x,
∴所求几何体的侧面积S=x(20-x)+$\frac{3}{4}×2π×\frac{\sqrt{2}}{2}$x(20-x)
=$(1+\frac{{3\sqrt{2}}}{4}π)x(20-x)$
$\begin{array}{l}=(1+\frac{{3\sqrt{2}}}{4}π)[-{x^2}+20x]\\=(1+\frac{{3\sqrt{2}}}{4}π)[-{(x-10)^2}+100]\end{array}$
∴当x=10时,${S_{max}}=75\sqrt{3}π+100$.)
即这个圆柱形木块剩下部分(如图一)侧面积的最大值为$75\sqrt{3}π+100$.
点评 本题考查了圆柱的侧面积及其性质、矩形的性质、二次函数的单调性,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{16}-\frac{y^2}{4}=1$ | B. | $\frac{x^2}{8}-\frac{y^2}{4}=1$ | C. | $\frac{x^2}{4}-{y^2}=1$ | D. | $\frac{x^2}{2}-{y^2}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
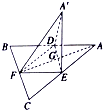 如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A'DE是△ADE绕DE旋转过程中的一个图形,则下列命题中正确的是( )
如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A'DE是△ADE绕DE旋转过程中的一个图形,则下列命题中正确的是( )| A. | ① | B. | ①② | C. | ①②③ | D. | ②③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com