Question

设函数f（x）=（其中常数a＞0，且a≠1）．
（1）当a=10时，解关于x的方程f（x）=m（其中常数m＞2）；
（2）若函数f（x）在（-∞，2]上的最小值是一个与a无关的常数，求实数a的取值范围．

Answer 1

解：（1）f（x）=（2分）
①当x＜0时，f（x）=＞3．因为m＞2．
则当2＜m≤3时，方程f（x）=m无解；
当m＞3，由10^x=，得x=lg．（4分）
②当x≥0时，10^x≥1．由f（x）=m得10^x+=m，
∴（10^x）²-m10^x+2=0．
因为m＞2，判别式△=m²-8＞0，解得10^x=．
因为m＞2，所以＞＞1．
所以由10^x=，解得x=lg．
令=1，得m=3．
所以当m＞3时，=＜=1，
当2＜m≤3时，=＞=1，解得x=lg．
综上，当m＞3时，方程f（x）=m有两解x=lg和x=lg；
当2＜m≤3时，方程f（x）=m有两解x=lg．（8分）

（2）①若0＜a＜1，
当x＜0时，0＜f（x）=＜3；
当0≤x≤2时，f（x）=a^x+．
令t=a^x，则t∈[a²，1]，g（t）=t+在[a²，1]上单调递减，
所以当t=1，即x=0时f（x）取得最小值为3．
当t=a²时，f（x）取得最大值为．
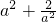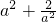此时f（x）在（-∞，2]上的值域是（0，]，没有最小值．（11分）
②若a＞1，
当x＜0时，f（x）=＞3；
当0≤x≤2时f（x）=a^x+．
令t=a^x，g（t）=t+，则t∈[1，a²]．
①若a²≤，g（t）=t+在[1，a²]上单调递减，
所以当t=a²即x=2时f（x）取最小值a²+，最小值与a有关；（13分）
②a²＞，g（t）=t+在[1，]上单调递减，在[，a²]上单调递增，
所以当t=即x=log_a时f（x）取最小值2，最小值与a无关．（15分）
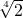综上所述，当a≥时，f（x）在（-∞，2]上的最小值与a无关．（16分）
分析：（1）当a=10时，f（x）=按照分段函数选择解析式，
①当x＜0时，f（x）=＞3．因为m＞2．所以当2＜m≤3时，方程f（x）=m无解；当m＞3，由10^x=求解．
②当x≥0时，10^x≥1．由f（x）=m得10^x+=m，转化为（10^x）²-m10^x+2=0．求解．
（2）根据题意有g（x）=a^|x|+2a^x，x∈[-2，+∞），根据指数函数，分①当a＞1时，②当0＜a＜1时，两种情况分析，每种情况下，根据绝对值，再按照x≥0时和-2≤x＜0两种情况讨论．最后综合取并集．
点评：本题主要考查了函数与方程的综合运用，主要涉及了方程的根，函数的最值等问题，还考查了分类讨论思想，转化思想．