
(1)y=cos2x+2sinx-2;(2)y=![]() .
.
(1)解:y=cos2x+2sinx-2=-sin2x+2sinx-1=-(sinx-1)2.
∵-1≤sinx≤1,
∴sinx-1∈[-2,0].
∴y∈[-4,0].
∴函数y=cos2x+2sinx-2的值域是[-4,0].
(2)解法一:∵y=![]() =1+
=1+![]() ,
,
∴当sinx=-1时,ymin=1+![]() =
=![]() .
.
∴值域为[![]() ,+∞).
,+∞).
解法二:由y=![]() ,得sinx=
,得sinx=![]() .
.
又∵-1≤sinx≤1,
∴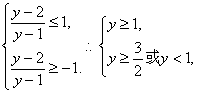 ∴y≥
∴y≥![]() .
.
∴函数y=![]() 的值域为[
的值域为[![]() ,+∞).
,+∞).
温馨提示
(1)一般函数的值域求法有:观察法、配方法、判别式法、反比例函数法等,而三角函数是函数的特殊形式,用上述方法时,要注意三角函数的特性.
(2)求三角函数的值域,主要是运用sinx,cosx的有界性,以及复合函数的有关性质.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| 1+sinx |
| 2+cosx |
| ex-e-x |
| ex+e-x |
| 1 |
| x |
| ||
| x+2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com