解:(1)由题得f(x)=x+

+a,设1≤x
1<x
2,
则

…
因为1≤x
1<x
2,所以x
1-x
2<0.所以f(x
1)-f(x
2)<0
所以f(x
1)<f(x
2),即f(x)在[1,+∞)上为增函数.…
(2)由(1)得:f(x)在[1,+∞)上为增函数,要满足f(3m)>f(5-2m),
只要1≤5-2m<3m,得1<m≤2
(3)g(x)=xf(x)=x
2+ax+a,由g(x)+2x+

>0得:

,即

①
因为x∈[2,5]时,x+1∈[3,6],那么①式可转化为

…
所以题目等价于化为

在x∈[2,5]上恒成立.即a大于函数

在x∈[2,5]上的最大值.
即求

在x∈[2,5]上的最小值.
令t=x+1,则t∈[3,6],所以

,由(1)得

,
在t∈[3,6],上为增函数,所以最小值为
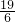
.所以-

.
分析:(1)利用函数单调性定义去证明函数的单调性.
(2)利用(1)的证明结论,利用函数的单调性求参数m的取值范.
(3)要使g(x)+2x+

>0恒成立,实质是最值恒成立,只需求出函数g(x)+2x+

的最小值即可,在求最小值的过程中可以使用基本不等式来求.
点评:本题考查了函数的单调性的定义以及函数单调性的应用.不等式恒成立往往转为最值恒成立.求函数的最值,可以使用导数,单调性以及基本不等式等方法去求最值.

 +a,x∈[1,+∞),且a<1
+a,x∈[1,+∞),且a<1 >0恒成立,求实数a的取值范围.
>0恒成立,求实数a的取值范围. +a,设1≤x1<x2,
+a,设1≤x1<x2, …
… >0得:
>0得: ,即
,即 ①
① …
… 在x∈[2,5]上恒成立.即a大于函数
在x∈[2,5]上恒成立.即a大于函数 在x∈[2,5]上的最大值.
在x∈[2,5]上的最大值. 在x∈[2,5]上的最小值.
在x∈[2,5]上的最小值.  ,由(1)得
,由(1)得 ,
,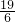 .所以-
.所以- .
.  >0恒成立,实质是最值恒成立,只需求出函数g(x)+2x+
>0恒成立,实质是最值恒成立,只需求出函数g(x)+2x+ 的最小值即可,在求最小值的过程中可以使用基本不等式来求.
的最小值即可,在求最小值的过程中可以使用基本不等式来求.

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<