解:(Ⅰ)y=f(x)-g(x)=mx-

-2lnx,y′=
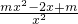
,
由于y=f(x)-g(x)在其定义域内为单调函数,则mx
2-2x+m≥0或者mx
2-2x+m≤0在[1,+∞)上恒成立,
即m

或者m

在[1,+∞)上恒成立,
而0<
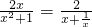
≤1,故m≥1或者m≤0,
综上,m的取值范围是(-∞,0]∪[1,+∞).
(Ⅱ)构造函数F(x)=f(x)-g(x)-h(x),F(x)=mx-

-2lnx-
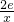
,
①当m≤0时,由x∈[1,e]得,mx-

≤0,-2lnx-
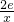
<0,
所以在[1,e]上不存在一个x
0,使得f(x
0)-g(x
0)>h(x
0);
②当m>0时,F′(x)=m+
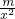
-

+

=

,
因为x∈[1,e],所以2e-2x≥0,mx
2+m>0,所以F′(x)>0在[1,+∞)上恒成立,故F(x)在x∈[1,e]上单调递增,
F(x)
max=me-

-4,只要me-

-4>0,解得m>
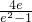
,
故m的取值范围是(
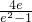
,+∞).
分析:(Ⅰ)y=f(x)-g(x)在[1,+∞)上为单调函数,即y′≥0或y′≤0在[1,+∞)上恒成立,从而转化为函数最值处理;
(Ⅱ)构造函数F(x)=f(x)-g(x)-h(x),则在[1,e]上至少存在一个x
0,使得f(x
0)-g(x
0)>h(x
0)成立,等价于x∈[1,e]时,F(x)
max>0,进而转化为求函数最大值问题.
点评:本题考查应用导数研究函数的单调性、最值问题,考查学生分析问题解决问题的能力.

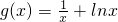 ,
, .
.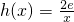 ,若在[1,e]上至少存在一个x0,使得f(x0)-g(x0)>h(x0)成立,求m的取值范围.
,若在[1,e]上至少存在一个x0,使得f(x0)-g(x0)>h(x0)成立,求m的取值范围. -2lnx,y′=
-2lnx,y′=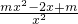 ,
, 或者m
或者m 在[1,+∞)上恒成立,
在[1,+∞)上恒成立,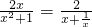 ≤1,故m≥1或者m≤0,
≤1,故m≥1或者m≤0, -2lnx-
-2lnx-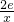 ,
, ≤0,-2lnx-
≤0,-2lnx-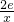 <0,
<0,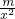 -
- +
+ =
= ,
, -4,只要me-
-4,只要me- -4>0,解得m>
-4>0,解得m>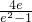 ,
,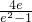 ,+∞).
,+∞).
