
正态总体当μ=0,σ=1时的概率密度函数是
f(x)=![]()
![]() ,x∈R.
,x∈R.
(1)证明f(x)是偶函数;
(2)求f(x)的最大值;
(3)利用指数函数的性质说明f(x)的增减性.
|
思路 用定义判定奇偶性,用单调性法求最值,用增减性的定义结合指数函数性质判定增减性. 解答 (1)对于任意的x∈R, f(-x)= 所以f(x)是偶函数. (2)令z= (3)任取x1<0,x2<0,且x1<x2,有 所以 所以 即f(x1)<f(x2). 它表明当x<0时,f(x)是递增的. 同理可得,对于任取的x1>0,x2>0,且x1<x2,那么有f(x1)>f(x2),即x>0时,f(x)是递减的. 评析 本题主要考查统计的基础知识及函数的性质. |


 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源:导学大课堂选修数学2-3苏教版 苏教版 题型:044
设任一正态总体N(μ,σ2)中取值小于x的概率为F(x),标准正态总体N(0,1)中,取值小于x0的概率为Φ(x0).
(1)证明F(x)可化为Φ(x0)计算;
(2)利用正态曲线的性质说明:当x取何值时,正态总体N(μ,σ2)相应的函数f(x)=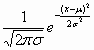 (x∈R)有最大值,其最大值是多少?
(x∈R)有最大值,其最大值是多少?
查看答案和解析>>
科目:高中数学 来源:导学大课堂选修数学2-3苏教版 苏教版 题型:044
正态总体当μ=0,σ=1时的概率密度函数是f(x)=![]() ,x∈R,
,x∈R,
(1)证明f(x)是偶函数;
(2)求f(x)的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com