
 ,②当x∈(-1,0)时,有f(x)>0;若
,②当x∈(-1,0)时,有f(x)>0;若 ,
, ,R=f(0),则P,Q,R的大小关系为________(用“<”连接)
,R=f(0),则P,Q,R的大小关系为________(用“<”连接) ),当x<y时,-1<
),当x<y时,-1< <0,同时有xy<1,可得f(x)-f(y)=f(
<0,同时有xy<1,可得f(x)-f(y)=f( )>0,即f(x)-f(y)>0,可得f(x)为减函数,进而分析P可得,P=f(
)>0,即f(x)-f(y)>0,可得f(x)为减函数,进而分析P可得,P=f( )-f(
)-f( )+f(
)+f( )-f(
)-f( )+…+f(
)+…+f(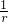 )-f(
)-f( )+…+f(
)+…+f( )-f(
)-f( ),消项可得p=f(
),消项可得p=f( )-f(
)-f( )=f(
)=f( )=f(
)=f( ),结合函数的单调性,可得答案.
),结合函数的单调性,可得答案. <1,
<1, <0,此时有f(x)-f(y)=f(
<0,此时有f(x)-f(y)=f( )>0,即f(x)-f(y)>0,
)>0,即f(x)-f(y)>0, )=f(
)=f( )=f(
)=f(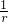 )-f(
)-f( ),
), )-f(
)-f( )+f(
)+f( )-f(
)-f( )+…+f(
)+…+f(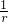 )-f(
)-f( )+…+f(
)+…+f( )-f(
)-f( )=f(
)=f( )-f(
)-f( )=f(
)=f( )=f(
)=f( ),
), <
< ,根据f(x)为减函数,
,根据f(x)为减函数, )>f(
)>f( ),
),

科目:高中数学 来源: 题型:
| ax+b |
| 1+x2 |
| 1 |
| 2 |
| 2 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)证明f(x)在[-1,1]上是增函数;
(2)解不等式f(x+![]() )<f(
)<f(![]() ).
).
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省青岛市即墨一中高一(上)期中数学试卷(解析版) 题型:解答题
 是定义在(-1,1)的奇函数,且f(
是定义在(-1,1)的奇函数,且f( )=
)= .
.查看答案和解析>>
科目:高中数学 来源:2009-2010学年黑龙江省哈尔滨三中高一(上)段考数学试卷(解析版) 题型:解答题
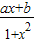 是定义在(-1,1)的奇函数,且f(
是定义在(-1,1)的奇函数,且f( )=
)= .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com